Geometry: The AAS Theorem
The AAS Theorem
You've accepted several postulates in this section. That's enough faith for a while. It's time for your first theorem, which will come in handy when trying to establish the congruence of two triangles.
- Theorem 12.2: The AAS Theorem. If two angles and a nonincluded side of one triangle are congruent to two angles and a nonincluded side of a second triangle, then the triangles are congruent.
Figure 12.7 will help you visualize the situation. In the following formal proof, you will relate two angles and a nonincluded side of ∠AB to two angles and a nonincluded side of ΔRST.
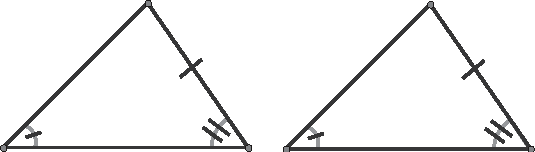
Figure 12.7Two angles and a nonincluded side of ΔABC are congruent to two angles and a nonincluded side of ΔRST.
- Given: Two triangles, ΔABC and ΔRST, with ∠A ~= ∠R , ∠C ~= ∠T , and ¯BC ~= ¯ST.
- Prove: ΔABC ~= ΔRST.
- Proof: You need a game plan. If only you knew about two angles and the included side! Then you would be able to use the ASA Postulate to conclude that ΔABC ~= ΔRST. But wait a minute! Because the measures of the interiorangles of a triangle add up to 180º, and you know two of the angles in are congruent to two of the angles in ΔRST, you can show that the third angle of ΔABC is congruent to the third angle in ΔRST. Then you'll have two angles and the included side of ΔABC congruent to two angles and the included side of ΔRST, and you're home free.
| Statements | Reasons | |
|---|---|---|
| 1. | ΔABC and ΔRST with ∠A ~= ∠R , ∠C ~= ∠T , and ¯BC ~= ¯ST. | Given |
| 2. | m∠A = m∠R and m∠C = m∠T | Definition of ~= |
| 3. | m∠A + m∠B + m∠C = 180º and m∠R + m∠S + m∠T = 180º | Theorem 11.1 |
| 4. | m∠A + m∠B + m∠C = m∠R + m∠S + m∠T | Substitution (step 3) |
| 5. | m∠A + m∠B + m∠C = m∠A + m∠S + m∠C | Substitution (steps 2 and 4) |
| 6. | m∠B = m∠S | Algebra |
| 7. | ∠B ~= ∠S | Definition of ~= |
| 8. | ΔABC ~= ΔRST | ASA Postulate |
The HL Theorem for Right Triangles
Whenever you are given a right triangle, you have lots of tools to use to pick out important information. For example, not only do you know that one of the angles of the triangle is a right angle, but you know that the other two angles must be acute angles. You also have the Pythagorean Theorem that you can apply at will. Finally, you know that the two legs of the triangle are perpendicular to each other. You've made use of the perpendicularity of the legs in the last two proofs you wrote on your own. Now it's time to make use of the Pythagorean Theorem.
- Theorem 12.3: The HL Theorem for Right Triangles. If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of a second right triangle, then the triangles are congruent.
There are several ways to prove this problem, but none of them involve using an SSA Theorem. Your plate is so full with initialized theorems that you're out of room. Not to mention the fact that a SSA relationship between two triangles is not enough to guarantee that they are congruent. If you use the Pythagorean Theorem, you can show that the other legs of the right triangles must also be congruent. Then it's just a matter of using the SSS Postulate.
Figure 12.8 illustrates this situation. You have two right triangles, ΔABC and ΔRST.
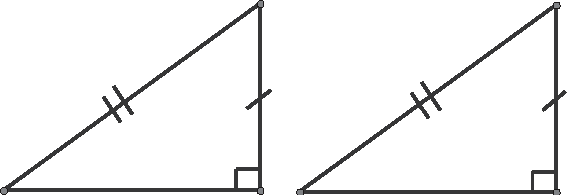
Figure 12.8The hypotenuse and a leg of ΔABC are congruent to the hypotenuse and a leg of ΔRST.
- Given: ΔABC and ΔRST are right triangles with ¯AB ~= ¯RS and ¯BC ~= ¯ST.
- Prove: ΔABC ~= ΔRST.
- Proof: You already have a game plan, so all that's left is to execute it.
| Statements | Reasons | |
|---|---|---|
| 1. | ΔABC and ΔRST are right triangles with ¯AB ~= ¯RS and ¯~= ¯ST. | Given |
| 2. | AB = RS and BC = ST | Definition of ~= |
| 3. | (AC)2 + (BC)2 and (RT)2 + (ST)2 = (RS)2 | The Pythagorean Theorem |
| 4. | (AC)2 + (BC)2 = (RT)2 + (ST)2 | Substitution (steps 2 and 3) |
| 5. | (AC)2 + (ST)2 = (RT)2 + (ST)2 | Substitution (steps 2 and 4) |
| 6. | (AC)2 = (RT)2 | Algebra |
| 7. | AC = RT | Algebra |
| 8. | ¯AC ~= ¯RT | Definition of ~= |
| 9. | ΔABC ~= ΔRST | SSS Postulate |
Tangled Knot
SSS, SAS, ASA, and AAS are valid methods of proving triangles congruent, but SSA and AAA are not valid methods and cannot be used. In Figure 12.9, the two triangles are marked to show SSA, yet the two triangles are not congruent. Figure 12.10 shows two triangles marked AAA, but these two triangles are also not congruent.
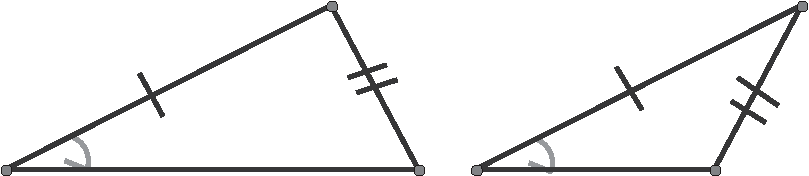
Figure 12.9These two triangles are not congruent, even though two corresponding sides and an angle are congruent. The two congruent sides do not include the congruent angle!
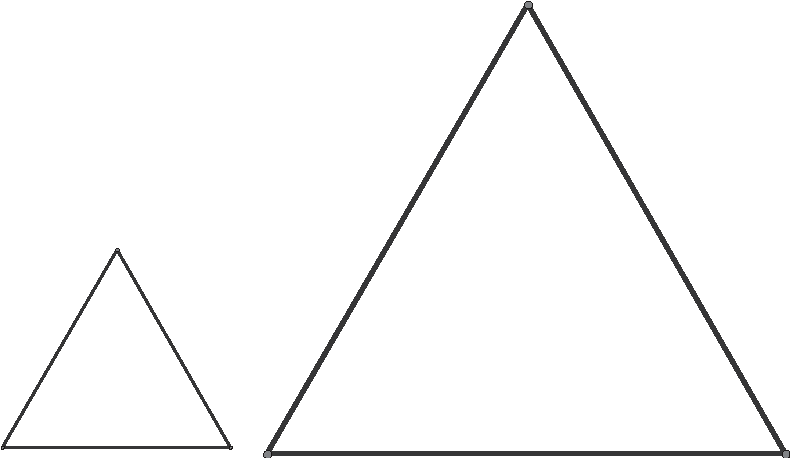
Figure 12.10These two triangles are not congruent, even though all three corresponding angles are congruent.
Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







