Geometry: Taxi-Cab Geometry
Taxi-Cab Geometry
Taxi-cab geometry does not owe its existence to contradicting Euclid's 5th Postulate. Instead, this geometry has its origins in mathematicians using different methods to measure distances. The following story is one possible scenario for how taxi-cab geometry came into existence.
The Joint Meetings of the American Mathematical Society and the Mathematics Association of America has been scheduled to occur in New York City. Mathematicians arrive in droves, each of them taking a cab from the airport to their hotel. The cab fare they pay depends on the distance traveled. One financially conservative mathematician looks at a tourist map he picked up at the airport and calculates the distance between the airport and the hotel to be 12.6 miles. The rates posted on the window of the cab indicate that the fare charged is $1.00 for the first tenth of a mile and twenty cents for every tenth of a mile thereafter. After a quick calculation, the mathematician expects the total fare to be $26.00 (not including tip).
The mathematician gets $30.00 out to cover the cab ride and the tip. He is shocked when the cabby tells him the fare is $48.00. This cannot be! He calculated the distance between the airport and the hotel using Euclid's notion of distance (as interpreted in the Cartesian Coordinate System) to be 12.6 miles. Even if the map is a bit inaccurate, the difference between Euclid's notion of distance and the cabby's notion of distance are like night and day (at least to this financially conservative mathematician).
Being a good citizen, the mathematician pays the cabby what is owed, but throughout the conference he tries to understand why his estimate of the fare was so far off base. Toward the end of the conference, he finally understands that he measured the distance between the airport and the hotel “as the crow flies,” whereas the cab must stick to the streets. The mathematician quickly establishes the rules for calculating distance in the taxi-cab world, and taxi-cab geometry is formed.
However taxi-cab geometry came about, it is interesting to note that if you redefine distance, you redefine the geometrical world. You can calculate distances in the taxicab geometry easily if you put your map on a Cartesian Coordinate System. Suppose you have two points, one with coordinates (1,3) and the other with coordinates (4,7), as shown in Figure 24.2. The distance between these points using the old-fashioned distance formula is found to be
- dEuclid = √(4 - 1)2 + (7 - 3)2
- dEuclid = √32 + 42
- dEuclid = √9 + 16
- dEuclid = √25
- dEuclid = 5
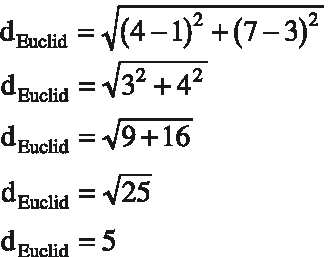
Figure 24.2The Cartesian Coordinate System with points having coordinates (1,3) and (4,7).
If you measure the distance between the two points using the taxi-cab metric, you will get dTaxi = 3 + 4 = 7.
Mathematicians usually write the taxi-cab distance formula as dTaxi. = a - c + b - d .
Eureka!
The taxi-cab distance between two points (a,b) and (c,d) is determined by the formula dTaxi. = a - c + b - d .
Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







