Geometry: Spherical Geometry
Spherical Geometry
In Euclidean geometry, two-dimensional construction occurs within a plane. Recall that if you are given any three noncollinear points, there exists a plane that contains them. It should not surprise you that with spherical geometry (or elliptic geometry), everything is done on a sphere. Lines are defined as the great circles that encompass the sphere. A great circle is a circle whose center lies at the center of the sphere, as shown in Figure 24.1. No matter how they are drawn, each pair of great circles will always intersect. As a result, parallel lines do not exist.
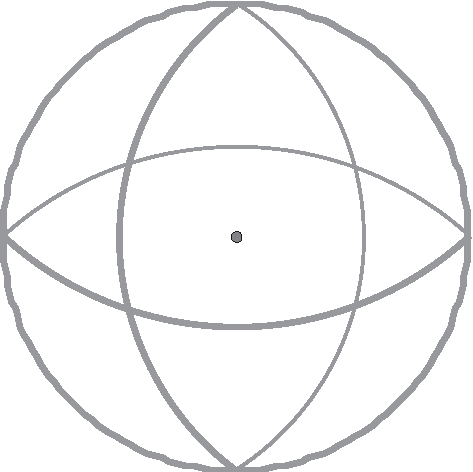
Figure 24.1A model of spherical geometry.
The mathematician Bernhard Riemann (1826−1866) is credited with the development of spherical geometry. Ironically enough, he was born about the same time that hyperbolic geometry was developed by Bolyai and Lobachevsky, and he was instrumental in convincing the mathematical world of the merits of non-Euclidean geometry.
Although hyperbolic geometry needed only to contradict the Parallel Postulate, spherical geometry doesn't get off so easy. There are three changes in Euclid's axiomatic system necessary to successfully create spherical geometry. Remember that lines in Euclidean geometry are the great circles in spherical geometry.
Tangent Line
Spherical geometry is important in navigation, because the shortest distance between two points on a sphere is the path along a great circle.
- Riemannian Postulate: Given a line and a point not on the line, every line passing though the point intersects the line. (There are no parallel lines).
All lines have the same finite length. (All great circles have a finite length: the circumference of the circles they describe.)
All perpendiculars to a straight line must meet at the same point.
This third postulate goes against our Euclidean intuition that if two lines are perpendicular to a third line, then the two perpendiculars are parallel. In spherical geometry, because there are no parallel lines, these two perpendiculars must intersect. But there is something more subtle involved in this third postulate. All perpendiculars meet at the same point. In this geometry, several counter-intuitive results follow. Some of these results are the same as the results in hyperbolic geometry, but for different reasons.
- The sum of the measures of the interior angles of a triangle is greater than 180º.
- All straight lines are bounded and finite in length.
- Rectangles do not exist.
- Two triangles with congruent corresponding angles are congruent.
- There is an upper bound on the area of a triangle.
- The intersection of two distinct lines is always two points.
Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







