Geometry: How Many Shapes Can a Circle Have?

How Many Shapes Can a Circle Have?

You have already learned that a circle is the set of all points a fixed distance away from one specific point that is called the center of the circle. The notion of a circle depends heavily on what is meant by distance. If you change the way that you measure distance, you change the way that you draw a circle.

Using the familiar definition of distance, a circle has the shape you have come to associate with a circle. But a “circle” (by definition) has a different shape in the taxi-cab and max geometries. I will discuss the shape of a circle in these other two geometries, but please use this information wisely. If you are told to arrange the chairs in a room in the shape of a circle, use a Euclidean circle rather than a taxi-cab circle!

Let me remind you of what the unit circle looks like in Euclidean geometry (in the Cartesian Coordinate System), with the center of the circle located at the origin. The unit circle is the set of all points 1 unit away from the origin. Certainly the points (1,0), (0,1), (−1,0) and (0,−1) are all on the unit circle, because their Euclidean distance from the origin is 1 unit. But the following points are also on the unit circle

• (^√2/₂ , ^√2/₂) , (^√2/₂ , - ^√2/₂) , (- ^√2/₂ , ^√2/₂) and (- ^√2/₂ , - ^√2/₂)

And there are many more. Points like (¹/₂ , ^√3/₂) are also on the unit circle. Any point (a,b), where a² + b² = 1 lies on the Euclidean unit circle. Figure 24.3 shows the Euclidean unit circle. There are no surprises.

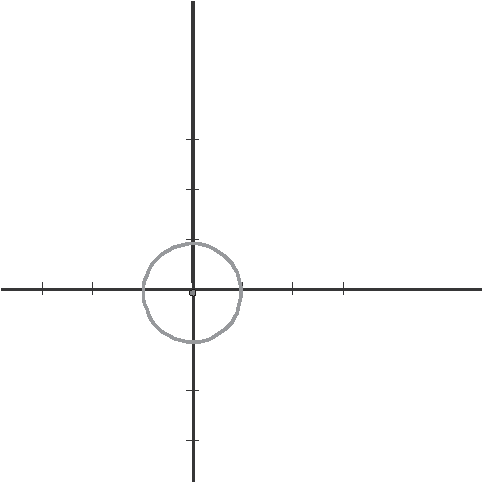
Figure 24.3The Euclidean unit circle.

Open your mind a bit, and let's try and visualize the taxi-cab unit circle centered at the origin. Think about the points that are 1 unit away from the origin using this new notion of distance. You could still travel to the points (1,0), (0,1), (−1,0) and (0,−1). So these points are on the Euclidean unit circle as well as the taxi-cab unit circle. Suppose now that you travel ¹/₂ unit to the right. How far up could you travel so that the total distance that the cab took you was 1 unit? You could travel up ¹/₂ unit, so that the total distance traveled was ¹/₂ + ¹/₂ = 1 unit. This is true whether you travel left or right first, and then up or down second. So the points (¹/₂ , ¹/₂) , (¹/₂ , - ¹/₂) , (- ¹/₂ , ¹/₂) , and (- ¹/₂ , - ¹/₂) are also on the taxi-cab unit circle. What if you traveled to the right ¹/₄ of a unit? Well, you could then travel ³/₄ of a unit up or down and you would have traveled a total distance of ¹/₄ + ³/₄ = 1 unit as well. So any point (a,b), where ‌ a ‌ + ‌ b ‌ = 1, lies on the taxi-cab unit circle. I have drawn the taxi-cab unit circle for you in Figure 24.4.

Figure 24.4The taxi-cab unit circle.

Notice that the resulting shape has some interesting properties. First of all, it is a quadrilateral. The next thing to observe is that the diagonals of this quadrilateral each have length 2, so they are congruent. Notice that the diagonals bisect each other. Finally, the opposite sides are congruent. Hey, this quadrilateral is a parallelogram, a rectangle, and a rhombus! It's a square! The taxi-cab unit circle has the shape of a Euclidean square! You can find the Euclidean length of the sides of this square: The Euclidean length is √2. So the taxi-cab unit circle is a Euclidean square with sides having length √2.

Finally, let's explore what a max unit circle centered at the origin looks like. Again, the points (1,0), (0,1), (−1,0) and (0,−1) are all on the max unit circle, because the maximum of the North/South and East/West distances is 1 unit. What about the point (1, ¹/₂? Is that point on the Max unit circle? Well, the Max distance between this point and the origin is d_Max = Max{1, ¹/₂} = 1, so the point (1,¹/₂ is on the max unit circle. What about the point (1,³/₄)? It's there as well. In fact, any point (a,b), where Max{ ‌ a ‌ , ‌ b ‌ } = 1 is on the max unit circle. So the point (-¹/₂,1) is on the Max unit circle. I have drawn the max unit circle for you in Figure 24.5.

Figure 24.5The Max unit circle.

Notice that the resulting shape has some interesting properties. First of all, the lines make up a quadrilateral. The next thing to observe is that the sides of this quadrilateral each have length 2, so they are congruent. Notice that two of the sides are horizontal lines, and the other two sides are vertical lines. So the sides of the quadrilateral are perpendicular, and they form a right angle. Hey, this quadrilateral is a parallelogram, a rectangle, and a rhombus! It's a square! The max unit circle has the shape of a Euclidean square, just like the taxi-cab unit circle was a square. But the max unit circle is a Euclidean square with side length 2, whereas the taxi-cab unit circle was a Euclidean square with sides having length √2. So the taxi-cab unit circle and the maxunit circle are both Euclidean squares with different lengths.