Chemistry: Effusion and Diffusion
Effusion and Diffusion
Other important behaviors of gases explained by the Kinetic Molecular Theory are effusion and diffusion. Effusion is the rate at which a gas escapes through a small hole in a container. Diffusion is the rate at which a gas travels across a room. Both of these phenomena are illustrated by the following figure.
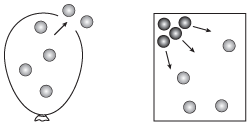
Figure 15.4(a) Effusion is when a gasescapes through a small hole in a container. (b) Diffusion is the rate at which a gas travels across the room.
The relative rates at which two gases effuse or diffuse is explained by Graham's Law, shown here:
- r1⁄r2 = √M2⁄M
The rate of motion of gas 1 is r1, and M1 denotes its molecular weight (in kg). Likewise, r2 and M2 stand for the rate of motion and molecular weight of gas 2. Let's see an example of how this equation is used:
You've Got Problems
Problem 2: I filled a balloon with H2 and found that it went flat in 16.0 hours. Using this information, how long will it take a balloon full of helium to go flat?
Example: If I pop a balloon of methane and a balloon of carbon dioxide at the same time, which gas will diffuse to the other end of the room more quickly?
Solution: We'll let r1 represent the rate of diffusion of methane and r2 represent the rate of diffusion of carbon dioxide. Plugging the molecular weights of both gases into this equation, we find that:
- rCH4⁄rCO2 = √0.0440kg / mol⁄0.0180kg / mol
We have determined that methane will travel across the room 1.56 times faster than carbon dioxide, making it the first to hit the opposite wall.
Excerpted from The Complete Idiot's Guide to Chemistry © 2003 by Ian Guch. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







