Geometry: When Is a Quadrilateral a Parallelogram?
When Is a Quadrilateral a Parallelogram?
I'm thinking of a quadrilateral with one pair of opposite sides parallel and congruent. Name that quadrilateral.
I'm thinking of a quadrilateral with both pairs of opposite sides congruent. Name that quadrilateral.
I'm thinking of a quadrilateral with both pairs of opposite angles congruent. Name that quadrilateral.
I'm thinking of a quadrilateral whose diagonals bisect each other. Name that quadrilateral.
If you answered “parallelogram” to all of the above, you are correct! Of course, by now you know that it's not enough to claim that I'm thinking of a parallelogram. There are doubters in the car, so you will have to prove it.
Opposite Sides Congruent and Parallel
Your first “Name That Quadrilateral” clue involved one pair of opposite sides being parallel and congruent. I'll call it a theorem and write a two-column proof. Figure 16.1 will help you visualize the situation.

Figure 16.1Quadrilateral ABCD with ¯BC and ¯BC ~= ¯AD.
- Theorem 16.1: If one pair of opposite sides of a quadrilateral are parallel and congruent, then the quadrilateral is a parallelogram.
Here's the game plan. Assume that ¯BC ¯AD and ¯BC ~= ¯AD. By definition, a parallelogram is a quadrilateral with both pairs of opposite sides parallel. You already know that one pair of opposite sides is parallel. You need to show that the other pair of opposite sides is parallel. In other words, you need to show that ¯AB ¯CD.
You can look at this quadrilateral in two ways. The first way is to focus on segments ¯BC and ¯AD cut by a transversal ¯AC. Then ∠BCA and ∠DAC are alternate interior angles and are congruent because ¯BC ¯AD. The second way is to turn it on its side. ¯AB and ¯CD are two segments cut by a transversal ¯AC. In this case, ∠BAC and ∠ACD are alternate interior angles. If you could show that ∠BAC ~= ∠ACD, then you could conclude that ¯AB ¯CD, and you would be done. The way to show ∠BAC ~= ∠ACD is to use CPOCTAC. In order to use CPOCTAC, you need to show ΔDAC ~= ΔBCA. In order to show ΔDAC ~= ΔBCA, you need to use the SAS Postulate. Let's write it up.
| Statements | Reasons | |
|---|---|---|
| 1. | Quadrilateral ABCD with ¯BC ¯AD and ¯BC ~= ¯AD. | Given |
| 2. | ¯BC ¯AD cut by a transversal ¯AC | Definition of transversal |
| 3. | ∠BAC and ∠ACD are alternate interior angles | Definition of alternate interior angles |
| 4. | ∠BCA ~= ∠DAC | Theorem 10.2 |
| 5. | ¯AC ~= ¯AC | Reflexive property of ~= |
| 6. | ΔDAC ~= ΔBCA | SAS Postulate |
| 7. | ∠BAC ~= ∠ACD | CPOCTAC |
| 8. | ¯AB and ¯CD are two segments cut by a transversal ¯AC | Definition of transversal |
| 9. | ∠BAC and ∠ACD are alternate interior angles | Definition of alternate interior angles |
| 10. | ¯AB ¯CD | Theorem 10.8 |
| 11. | Quadrilateral ABCD is a parallelogram | Definition of parallelogram |
Now that you have named that quadrilateral correctly, you can move on to the next quadrilateral.
Two Pairs of Congruent Sides
In the second “Name That Quadrilateral” game, the quadrilateral had two pairs of congruent sides. Let's write that as a theorem and lay it to rest.
- Theorem 16.2: If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
We have a visual in Figure 16.2. We have a parallelogram ABCD with ¯AB ~= ¯CD and ¯BC ~= ¯AD. The game plan is to divide the quadrilateral into two triangles using the diagonal ¯AC. Use the SSS Postulate to show that the two triangles are congruent, and use CPOCTAC to conclude that alternate interior angles are congruent and opposite sides must be parallel. If we show this for both pairs of opposite sides, then we have a parallelogram by definition. It's time to write out the details.

Figure 16.2Quadrilateral ABCD with ¯AB ~= ¯CD and ¯BC ~= ¯AD
| Statements | Reasons | |
|---|---|---|
| 1. | Quadrilateral ABCD with ¯AB ~= ¯CD and ¯BC ~= ¯AD | Given |
| 2. | ¯AC ~= ¯AC | Reflexive property of ~= |
| 3. | ΔABC ~= ΔCDA | SSS Postulate |
| 4. | ∠BAC ~= ∠ACD and ∠BCA ~= ∠DAC | CPOCTAC |
| 5. | ¯BC and ¯AD are two segments cut by a transversal ¯AC | Definition of transversal |
| 6. | ∠BAC and ∠ACD are alternate interior angles | Definition of alternate interior angles |
| 7. | ¯BC ¯AD | Theorem 10.8 |
| 8. | ¯AB and ¯CD are two segments cut by a transversal ¯AC | Definition of transversal |
| 9. | ∠BAC and ∠ACD are alternate interior angles | Definition of alternate interior angles |
| 10. | ¯AB ¯CD | Theorem 10.8 |
| 11. | Quadrilateral ABCD is a parallelogram | Definition of parallelogram |
Once again, the sweet taste of victory! You have named that quadrilateral correctly. Next!
Two Pairs of Congruent Angles
The third description of the quadrilateral involved both pairs of opposite angles being congruent. I'll state the theorem and use Figure 16.3 to guide you through your proof.
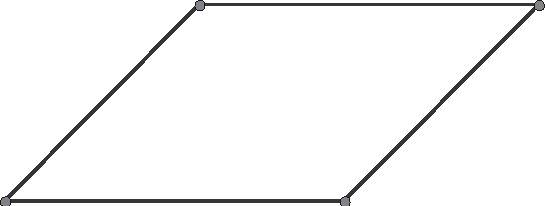
Figure 16.3Quadrilateral ABCD with ∠A ~= ∠C and ∠B ~= ∠D.
- Theorem 16.3: If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
You need to start with your angles. Because the measures of the sums of the interior angles of a quadrilateral add up to 360º, you can show m∠A + m∠B = 180º , or that ∠A and ∠B are supplementary angles. Now, you can look at this quadrilateral in the following light: ¯BC and ¯AD are two segments cut by a transversal ¯AB. Usually the transversal has been ¯AC, but this time you'll use ¯AB. Because your two angles on the same side of the transversal are supplementary, Theorem 10.10 tells you that ¯BC ¯AD. A similar argument shows that ¯AB ¯CD.
| Statements | Reasons | |
|---|---|---|
| 1. | Quadrilateral ABCD with ∠A ~= ∠C and ∠B ~= ∠D | Given |
| 2. | m∠A + m∠B + m∠C + m∠D = 360º | The measures of the interior angles of a quadrilateral add up to 360º |
| 3. | m∠A + m∠B + m∠A + m∠B = 360º | Substitution (steps 1 and 2) |
| 4. | m∠A + m∠B = 180º | Algebra |
| 5. | ∠A and ∠B are supplementary angles | Definition of supplementary angles |
| 6. | ¯BC and ¯AD are two segments cut by a transversal ¯AB | Definition of transversal |
| 7. | ¯BC ¯AD | Theorem 10.10 |
| 8. | ¯AB and ¯CD are two segments cut by a transversal ¯AD | Definition of transversal |
| 9. | m∠A + m∠D = 180º | Substitution (steps 1 and 4) |
| 10. | ∠A and ∠D are supplementary angles | Definition of supplementary angles |
| 11. | ¯AB ¯CD | Theorem 10.10 |
| 12. | Quadrilateral ABCD is a parallelogram | Definition of parallelogram |
Bisecting Diagonals
Ah, the last name game of this series! If you have a quadrilateral that has diagonals that bisect each other, your quadrilateral is a parallelogram. Figure 16.4 shows a parallelogram ABCD with diagonals ¯AC and ¯BD that intersect at M and bisect each other.

Figure 16.4Quadrilateral ABCD with diagonals ¯AC and ¯BD that intersect at M and bisect each other.
- Theorem 16.4: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
If you look at Figure 16.4, the game plan for proving this theorem should be coming through loud and clear. You will make use of Theorem 16.2: Pairs of opposite sides of a parallelogram are congruent. The two diagonals divide the parallelogram into four triangles. Because the diagonals bisect each other, ¯AM ~= ¯MC and ¯BM ~= ¯MD. Because vertical angles are congruent, you can use the SAS Postulate to show that ΔAMB ~= ΔBMC and ΔAMB ~= ΔDMC. From there it's a matter of applying CPOCTAC to show that both pairs of opposite sides are congruent.
| Statements | Reasons | |
|---|---|---|
| 1. | Quadrilateral ABCD with diagonals ¯AC and ¯BD that intersect at M and bisect each other | Given |
| 2. | ¯AM ~= ¯MC and ¯BM ~= ¯MD | Definition of bisection |
| 3. | ∠AMB ~= ∠CMD and ∠AMD ~= ∠BMC | Theorem 8.1 |
| 4. | ΔAMD ~= ΔBMC and ΔAMB ~= ΔDMC | SAS Postulate |
| 5. | ¯BC ~= ¯AD and ¯AB ~= ¯CD | CPOCTAC |
| 6. | Quadrilateral ABCD is a parallelogram | Theorem 16.2 |
Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







