Geometry: When Is a Parallelogram a Rhombus?
When Is a Parallelogram a Rhombus?
I'm thinking of a parallelogram whose diagonals are perpendicular. Name that parallelogram.
If you guessed that it was a square, then you didn't read the heading for this section very well. It's a rhombus! The nice thing about working with parallelograms is that the diagonals create lots of triangles just begging to be proven congruent. In Figure 16.6, parallelogram ABCD has perpendicular diagonals. The congruent triangles are trying to communicate with you. Listen closely.

Figure 16.6Parallelogram ABCD with ¯AC ⊥ ¯BD.
- Theorem 16.6: If the diagonals of a parallelogram are perpendicular, the parallelogram is a rhombus.
Let's just jump right into the game plan. You know that ¯AC ⊥ ¯BD, so m∠AMB = 90º and m∠CMB = 90º. Because the diagonals of a parallelogram bisect each other, you know that ¯AM ~= ¯MC. The reflexive property of ~= enables you to write ¯BM ~= ¯BM. By the SAS Postulate, you know that ΔAMB ~= ΔCMB. By CPOCTAC, you know that ¯AB ~= ¯BC. Because ¯AB ~= ¯BC and ¯AB ~= ¯BC are adjacent sides, you have a parallelogram with congruent adjacent sides, a.k.a. a rhombus.
| Statements | Reasons | |
|---|---|---|
| 1. | Parallelogram ABCD has ¯AC ⊥ ¯BD | Given |
| 2. | ∠AMB and ∠CMB are right | Definition of ⊥ |
| 3. | m∠AMB = 90º and m∠CMB = 90º | Definition of right angle |
| 4. | ∠AMB ~= ∠CMB | Definition of ~= |
| 5. | ¯AM ~= ¯MC | Theorem 15.6 |
| 6. | ¯BM ~= ¯BM | Reflexive property of ~= |
| 7. | ΔAMB ~= ΔCMB | SAS Postulate |
| 8. | ¯AB ~= ¯BC | CPOCTAC |
| 9. | Parallelogram ABCD is a rhombus | Definition of rhombus |
Now let's get a little tricky. Suppose you have a rectangle ABCD. Find the midpoints of each of the sides of the rectangle and join them together consecutively to form the quadrilateral MNOP, as shown in Figure 16.7. What kind of quadrilateral is made?
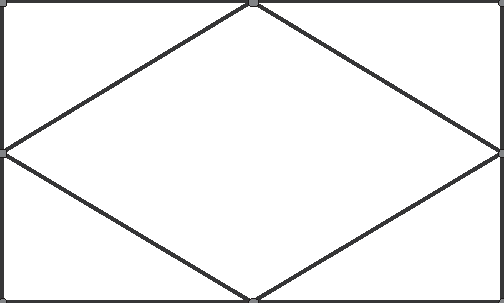
Figure 16.7Rectangle ABCD, with midpoints of each side joined together consecutively to form the quadrilateral MNOP.
From the picture, it looks kind of like a parallelogram. You have to be careful, though, because looks can be deceiving. It also looks like the diagonals of the newly created quadrilateral are perpendicular. If the drawing is accurate, you might be tempted to conclude that the quadrilateral is a rhombus. Let's prove it.
- Theorem 16.7: If the midpoints of the sides of a rectangle are joined in order, the quadrilateral formed is a rhombus.
You need a serious game plan for this one. Because M, N, O, and P are the midpoints of ¯AB, ¯BC, ¯CD, and ¯AD, you know that ¯BN ~= ¯NC ~= ¯AP ~= ¯PD and ¯AM ~= ¯MB ~= ¯OD ~= ¯CO. Because you're dealing with a rectangle, you know that m∠A = 90º, m∠B = 90º , m∠C = 90º, and m∠D = 90º. So by the SAS Postulate, ΔPAM ~= ΔNBM ~= ΔPDO ~= ΔNCO. Applying the CPOCTAC principal ¯MN ~= ¯MP ~= ¯PO ~= ¯NO. So opposite sides are congruent and quadrilateral MNOP is a parallelogram. Also, adjacent sides are congruent, so parallelogram MNOP is a rhombus.
| Statements | Reasons | |
|---|---|---|
| 1. | Rectangle ABCD, with midpoints of each side joined together consecutively to form the quadrilateral MNOP | Given |
| 2. | ¯BC ~= ¯NC, ¯AP ~= ¯PD, and ¯OD ~= ¯CO | Definition of midpoint |
| 3. | ¯AB ~= ¯CD and ¯BC ~= ¯AD | Theorem 15.4 |
| 4. | BN = 1/2BC, AP = 1/2AD, AM = 1/2AB and CO = 1/2CD | Theorem 9.1 |
| 5. | BN = NC = AP = PD and AM = MB = OD = CO | Substitution (steps 2, 3, 4) |
| 6. | ¯BN ~= ¯NC ~= ¯AP ~= ¯PD and ¯AM ~= ¯MB ~= ¯OD ~= ¯CO | Definition of ~= |
| 7. | m∠A = 90º. m∠B = 90º , m∠C = 90º and m∠D = 90º | Definition of rectangle |
| 8. | ΔPAM ~= ΔNBM ~= ΔPDO ~= ΔNCO | SAS Postulate |
| 9. | ¯MN ~= ¯MP ~= ¯PO ~= ¯NO | CPOCTAC |
| 10. | Quadrilateral MNOP is a parallelogram | Theorem 16.2 |
| 11. | Quadrilateral MNOP is a rhombus | Definition of rhombus |
Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







