Geometry: Three Famous Triangles

Three Famous Triangles

Now that you have developed the skills needed to prove either that two triangles are congruent or two triangles are similar, you can explore the properties of three of the most famous types of triangles: the 45-45-90 triangle, the 30-60-90 triangle, and the 60-60-60 triangle. Start with the equiangular triangle first.

60-60-60 Triangle

A 60-60-60 triangle is an equiangular triangle. If you look at the equiangular triangle in Figure 14.6, some observations are immediate. If you flip the triangle so that vertex A corresponds with vertex B, and vertex B corresponds to vertex A, then by the AA Similarity Theorem, ΔABC ~ ΔBAC. So what? Well, because CSSTAP, you see that

• ^BC/_AB = ^AC/_AB , so BC = AC.

You can flip the triangle again, so that vertex A corresponds to vertex C and vertex C corresponds to vertex A. Then using CSSTAP you have the proportionality

• ^AB/_AC = ^BC/_AC, or that AB = BC.

No matter how you slice it, all three sides of an equiangular triangle are congruent. So an equiangular triangle is an equilateral triangle, and an equilateral triangle is an equiangular triangle. I will state this as a theorem.

Figure 4.6ΔABC is an equiangular triangle.

• Theorem 14.3: Every equiangular triangle is an equilateral triangle, and every equilateral triangle is an equiangular triangle.

Now that you know that a 60-60-60 triangle is also an equilateral triangle, it's time to bisect this triangle and see what it's made of. Figure 14.7 shows an equiangular triangle ΔABC , with an altitude dropped from vertex B to side ¯AC. Call the point of intersection of the altitude and ¯AC to point D. Again, using the AA Similarity Theorem, you can show that ΔABD ~ ΔCBD. You can use the properties of similar triangles to show that

• ^AD/_AB = ^DC/_BC , or that AD = DC.

Because AD + DC = AC (by the Segment Addition Postulate), you see that D is the midpoint of ¯AC and that

• AD = ¹/₂AC.

Figure 14.7ΔABC with altitude →BD from B to ¯AC.

The interior angles of a triangle add up to 180º. If m∠BAD = 60º and m∠BDA = 90º, then m∠DBA = 30º. Because ΔABD ~ ΔCBD, you also know that m∠DBC = 30º, and that →BD (the altitude from B to ¯AC) bisects ∠ABC. You have also just created the second special triangle.

30-60-90 Triangle

The second special triangle is the 30-60-90 triangle. It can be created by taking an equilateral triangle and bisecting one angle. Figure 14.8 shows two 30-60-90 triangles formed by bisecting an equilateral triangle. These two triangles formed are congruent, and are worth further investigation.

Each of these triangles has two legs: one formed from one-half of the side of the equilateral triangle (either ¯AD or ¯DC, depending on the triangle) and the other formed by the altitude from vertex B to ¯AC (¯BD). You can use the Pythagorean Theorem to discover relationships between the lengths of the sides. Let's focus on ΔABD : If you let x represent AD, then AB = 2x, as shown in Figure 14.8. This is because all sides of an equilateral triangle are congruent, and when you divided ΔABC into two triangles, one of the sides was cut in half. Using the Pythagorean Theorem, you can find the length of the second leg:

• (AD)² + (BD)² = (AB)²
• (x)² + (BD)² = (2x)²
• (BD)² = 4x² - x² = 3x²
• BD = x√3

Figure 14.8ΔABD is a 30-60-90 triangle with AD = x.

Because √3 > 1 , you can see that the length of the leg opposite the 60º angle is bigger than the length of the leg opposite the 30º angle. I will state these results as a theorem:

• Theorem 14.4: In a 30-60-90 triangle, the hypotenuse has a length equal to twice the length of the leg opposite the shorter angle, and the length of the leg opposite the 60º angle is the product of √3 and the length of the shorter leg.

You can use these results to find the missing pieces.

• Example 3: Find the lengths of the missing sides of each triangle in Figure 14.9.

Figure 14.9ΔABC and ΔRST.

• Solution: Let's look at ΔABC first. Because the length of the hypotenuse isgiven to be 20, you know that the shorter leg has one-half this length. The shorter leg is the leg opposite the 30º angle, which is ¯AC. So AC = 10. The other leg (the one opposite the 60º angle) has length equal to the product of the length of the shorter leg and √3, so BC = 10√3.
• For ΔRST, things are a little trickier. You are given the length of the leg opposite the 60º angle, and you need to find the length of the shorter leg and the hypotenuse. Because RT = ST√3, and RT = 9, you have that 9 = ST√3, or ST = ⁹/_√3. The hypotenuse has length equal to twice the length of the shortest leg, so RS = 2 × 3√3 = 6√3.

45-45-90 Triangle

A 45-45-90 triangle has two acute angles with equal measure and one right angle. You can use the Pythagorean Theorem to find the relationships between the lengths of the legs and the length of the hypotenuse.

Figure 14.10 shows a typical 45-45-90 triangle. You can easily prove that the two legs are congruent by showing ΔABC ~= ΔBAC (using the SAS Postulate).

You can combine this result with the Pythagorean Theorem to determine the relationships between the length of one of the legs and the length of the hypotenuse. Because (AB)² = (BC)² + (AC)², and AC = BC, you have (AB)² = 2(BC)². Using the Square Root Property of Equality, you see that AB = BC√2.

Figure 14.10A typical 45-45-90 triangle.

You can use these relationships to find the missing pieces of the triangle.

• Example 4: Find the lengths of the missing sides in the triangle shown in Figure 14.11.

Figure 14.11ΔABC is a 45-45-90 triangle.

• Solution: Because the length of one of the legs is 8, the length of the hypotenuse is 8√2 and the length of the other leg is 8.

Here's your chance to shine. Remember that I am with you in spirit and have provided the answers to these questions in Answer Key.

1. Prove that if a line is parallel to one side of a triangle and passes through the midpoint of a second side, then it will pass through the midpoint of the third side.

2. Find the lengths of the missing sides of each triangle in Figure 14.12.

Figure 14.12ΔABC and ΔRST.

3. Find the lengths of the missing sides in the triangles shown in Figure 14.13.

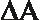
Figure 14.13ΔABC is a 45-45-90 triangle.