Geometry: The Tangent Ratio

The Tangent Ratio

Trigonometry got its start from calculations of early mathematicians and astronomers. They studied ratios of the lengths of the sides of right triangles and noticed some interesting things. For example, they observed that whenever the ratio of a shorter leg's length to the longer leg's length was 7/10 the angle opposite the shorter leg (that is, the smallest angle of the right triangle) was always 35º. Figure 20.1 shows a few triangles with leg length ratio 7/10. Notice that all of these triangles are similar. They each have a right angle, and they each have an angle of measure 35º. By the AA Similarity Theorem (Theorem 13.1), they are similar.

Figure 20.1Three right triangles, each having the ratio of the length of the shorter leg divided by the length of the longer leg equal to ⁷/₁₀.

But this doesn't just happen with the ratio 7/10. All right triangles with the same leg length ratio will be similar to each other.

Figure 20.2 shows a typical right triangle. Recall that ¯AB is the hypotenuse of the triangle. If you focus on ∠BAC , then ¯BC is the side opposite ∠BAC and ¯AC is the side adjacent to ∠BAC. If your focus was on ∠ABC, then the opposite side is ¯AC and the adjacent side is ¯BC. The nice thing about the hypotenuse is that it is always the sideopposite the right angle, and that never changes. The ratio of the length of the opposite side of an angle divided by the length of the adjacent side in a right triangle is called the tangent of the angle. Write

• tan ∠BAC = ^BC/_AC

when you want to say “the tangent of ∠BAC is the ratio ^BC/_AC.” When there is no confusion about the angle involved, you can shorten this notation to

• tan ∠A = ^BC/_AC.

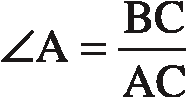
Figure 20.2A right triangle ΔABC.

Notice that in the triangle in Figure 20.2, tan ∠A = ^BC/_AC and tan∠B = ^AC/_BC. These tangent ratios are the reciprocals of each other! That means that if tan ∠A > 1, tan ∠B

If the tangent ratio of an angle is equal to 1, that means that the length of the opposite side equals the length of the adjacent side. You have a triangle with two legs of equal length. You've seen that triangle before; it's a 45-45-90 triangle.

If you interpret this triangle as an object (say a tree) making a shadow on the earth (as shown in Figure 20.3), then this 35º angle is referred to as the angle of elevation.

You have seen an application of this idea earlier in the section. Remember the find-the-tree-height problem in Similar Triangles? You solved this problem using similar triangles. You had the triangle formed by the tree and its shadow, and you had the triangle formed by you and your shadow. Using proportionalities, you were able to accurately estimate the height of the tree.

Figure 20.3A tree making a shadow on the earth can be interpreted as forming a right triangle.

You can change the situation a little. What if you did not know your height, but could estimate the angle of elevation?

• Example 1: Suppose that you have a tree, similar to the one shown in Figure 20.3. You are told that the angle of elevation is 30º and that tan 30º =.577. If the shadow of the tree is 25 feet, estimate the height of the tree.
• Solution: You know tan 30º =.577. You also know that tan 30º = ^BC/_AC. Using substitution (and the fact that AC = 25), you have
• ^BC/₂₅ =.577
• BC = 25(.577) = 14.4 feet.

Early mathematicians calculated tables of values for the tangent of various functions. When I learned trigonometry (many years ago), my textbook came with tables of tangent values for various angles. Calculations were much more tedious, because we didn't have calculators (not even the basic kind that just add, subtract, multiply, and divide).

These days, trig books don't even mention the existence of these tables, much less include them. That's because any scientific calculator (the only ones worth spending money on) has a tangent button (TAN). Depending on the kind of calculator you own, you will either just enter your angle measure and push the TAN button, or you'll push the TAN button, the angle measure, and the “enter” or “=” button. You'll get to practice finding the tangent of a variety of angles as you go on.