Geometry: The Sine Ratio
The Sine Ratio
The tangent function examined the values of the ratio of the two legs of the right triangle. You can also take the ratio of the length of one leg divided by the length of the hypotenuse. You have two legs, so which one should you use?
In a right triangle, every angle has an opposite side and an adjacent side. And there's always a hypotenuse. Don't forget the hypotenuse. If you work with the opposite side and the hypotenuse you are dealing with the sine ratio. The sine of an angle is the ratio of the length of the opposite side divided by the length of the hypotenuse.
Solid Facts
In a right triangle, the sine of an angle is the ratio of the length of the opposite side divided by the length of the hypotenuse.
Let's use the Pythagorean Theorem to explore some of the properties of the sine ratio. Given a right triangle (like the one shown in Figure 20.4), let the lengths of the triangle be a, b, and c, where a is the length of the side opposite ∠A, b is the length of the side opposite ∠B, and c is the length of the side opposite ∠C (and is the length of thehypotenuse). Then the Pythagorean Theorem tells you that a2 + b2 = c2. The sine of ∠A (which will be written sin ∠A) is the ratio of the length of the side opposite ∠A divided by the length of the hypotenuse; sin ∠A = a/c. Because a ≤ c, sin ∠A ≤ 1 (the only way sin∠A = 1 is if a = c, but that would make for a strange triangle!), the sine ratio cannot be greater than 1.

Figure 20.4A right triangle with side lengths a and b, and hypotenuse length c.
If you are given a right triangle, and you know the tangent of the angle, you can find the sine of the angle by applying the Pythagorean Theorem.
- Example 2: Suppose a right triangle has an angle with tangent ratio 5/12. Find the sine ratio of that angle.
- Solution: Figure 20.5 will help you visualize what is going on.
- You are given that tan ∠A = 5/12 so a = 5 and b = 12. You can use the Pythagorean Theorem to find the length of the hypotenuse:
- c2 = a2 + b2
- c2 = 52 + 122 = 25 + 144 = 169
- c = 13
Tangent Line
Let's explore the sine ratio for a right angle. The definition of the sine ratio is the ratio of the length of the opposite side divided by the length of the hypotenuse. Well, the length of the side opposite ∠C is the length of the hypotenuse, so sin ∠C = c/c = 1 Because ∠C is a right angle, m∠C = 90º, so sin 90º = 1.
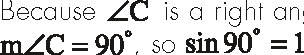
Figure 20.5A right triangle with tan ∠A = 5/12.
Now that you know the length of the hypotenuse, it is a simple matter of finding the sine ratio of that angle (it's the ratio of the length of the side opposite the angle divided by the length of the hypotenuse):
- sin ∠A = 5/13
This calculation works both ways. If you are given the sine ratio of an angle of a triangle, you can find the tangent ratio of the angle.
- Example 3: If a right triangle has an angle with a sine ratio of 4/5, find the tangent ratio of that angle.
- Solution: Let's take a look at Figure 20.6. In order to find the tangent ratio of the angle, you need to know the length of the side opposite the angle and the length of the side adjacent to the angle. Because the sine ratio is 3/5, the length ofthe side opposite the angle is 3 and the length of the hypotenuse is 5. Using the Pythagorean Theorem, you can solve for the length of the side adjacent to the angle:
- a2 + b2 = c2
- 32 + b2 = 52
- 9 + b2 = 25
- b2 = 16
- b = 4
So the tangent ratio is 3/4.
Figure 20.6A right triangle with an angle having a sine ratio of 3/5.
The Pythagorean Theorem will be used so often throughout this section that you will know it like the back of your hand by the time you are finished with this section!
Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







