Weather: Richardson's Experiment
Richardson's Experiment
Weather Words
"Science is the knowledge of consequences and the dependence of one fact upon another."
—Thomas Hobbes
At the start of the twentieth century, British meteorologist Lewis Fry Richardson had the idea of performing a mathematical solution of the complex mathematical representation of the atmosphere. He divided the world into checkerboard squares and attempted to calculate a 24-hour forecast. Unfortunately his forecast for "tomorrow" wasn't finished for about a year, and by the time it was finally complete, the weather was shown to move backward at the speed of sound! He didn't realize why his forecast went so badly. He was stumped. As a pacifist in World War I, he joined the ambulance corps and almost completely abandoned meteorology for decades. In 1922, his book Weather Prediction by Numerical Process was published. But his vision was far ahead of his time. Although that book was and remains a wonderful basic text in understanding the formulations that make the weather happen, little could be done with his concepts. Something went terribly wrong with Richardson's experiment, and he took up a new career in psychology. Later in this section, we'll see what went wrong.
Want to Try the Math?
Because the atmosphere is a physical system, it can be represented by mathematics. Ideally solving that math should provide the weather forecast for tomorrow. Several equations, or mathematical expressions, describe what is happening to the weather.
Newton's Law
The math really isn't that bad. Newton put down the basic laws of fluid motion. Accordingly, if a force is applied to the atmosphere, it should accelerate. For instance, if the pressure is greater at point A than point B, the air will move at an accelerating rate from A to B (see the following figure). That's all there is to it. In addition to pressure forces, there are other forces such as gravity, friction, and electricity. And a complete representation is needed to get an accurate picture of the atmosphere, although for ease of solution, pressure and gravity are the main players with friction tacked on later when we develop enough confidence in the process.
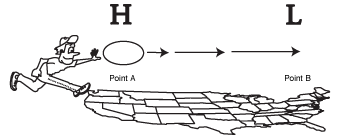
Newton's law of motion.
So a particular force exerted in the atmosphere makes it move. It doesn't get simpler than that. The motion is expressed in terms of acceleration, but that really says something about velocity, too, because acceleration is an expression of changing velocity. In any case, if we can measure the forces, we can calculate the velocity of the air—which, of course, is the wind. Newton's laws of motion can be applied to the total wind, or they can be broken up into three components—the wind that moves from west to east, the wind that comes from the south, and the air flow that moves vertically. Therefore there can be three expressions of Newton's laws: one for west-east motion, another for north-south motion, and the other for up-and-down motion.
It sounds okay, but the forces acting on the weather, especially pressure, will undergo change. If we're going to predict future wind from pressure, we need a way of predicting pressure changes. Newton's laws aren't quite enough.
Ideal Gas Law
During the seventeenth century, another important discovery was made. Robert Boyle came up with the assertion that the pressure of a gas depends on volume and temperature: the ideal gas law. So now we have an expression for figuring out future pressure—from the future volume and future temperature. What have we gained? Not a lot, really, because now we need to come up with expressions that show future volume and future temperature.
The volume is related to density, and the density can be derived from the concept of mass conservation. It's the jelly-sandwich principle. If you sit on a jelly sandwich, the jelly will come out at the sides. Similarly, if the air converges horizontally, it will be forced to move vertically. Changes in density can be computed by measuring the convergence. In many situations, that change in density is negligible because of the jelly-sandwich process. The sandwich could be squished, but the density of the jelly remains unchanged because there is a mass flow out the sides. If that flow were prevented, the density would change, but in the atmosphere, there's nothing to restrict that compensating motion. In most cases, the density change is very small.
Okay that takes care of density changes, but what about future temperature?
Thermodynamics
Weather-Speak
Thermodynamics is the study of heat and its transformation to mechanical energy.
Later in the nineteenth century, expressions that relate heat to temperature and volume were developed. In "Partly to Mostly Cloudy," we showed how a change in heat brings about a change in volume of a gas, along with a change in temperature. If a can is put on a stove and the burner is turned on, the air molecules inside the can move around. If they hit each other more frequently, the temperature goes up. But the molecules can also bang against the side of the can and force the can to expand. So if heat is added to a gas, it will expand and reach a higher temperature. Likewise, a change in temperature can be brought about by a change in volume or a change in heat. In other words, you can't get something for nothing—and that tells the story of the first law of thermodynamics.
With this thermodynamic expression, the new temperature could be found—but of course that can only be derived if we know the change of heat.
The Dilemma
Let's stop right here. It's getting too complicated. Every time we try to come up with a way of solving one of the variables, we end up introducing another one. You might ask, "What about the second law of thermodynamics?" Well, go ahead, use it. But you'll just introduce yet another unsolved variable—this time, entropy. It just never ends. And this underscores the problem of modern, objective mathematical weather forecasting. There are just too many variables. We always have at least one too many.
Here we have introduced Newton's Laws of Motion in three directions. That gives us three expressions. Then there are the ideal gas law, mass conservation, and the first law of thermodynamics. For these six expressions, we have seven unknowns: the wind blowing west to east, south to north, and vertically, the pressure, the density, the temperature, and the heat. It's an impossible situation—as soon as you try to simplify, there goes accuracy. No matter how many Doppler radars are available or satellites launched, the problem remains.
Still we can make the effort and at least approximate the future weather. Richardson tried and gave up. Another attempt was made about 25 years later, which really did usher in the second Renaissance.
Weather-Wise
I'm often asked about the accuracy of long-range weather predictions. I like to tell people not to depend too heavily on the details of the fourth and fifth day of the five-day forecast. The extended forecasts should be used for trends rather than specifics. My reason: There are seven basic variables and only six equations to solve for the seven unknowns.
Richardson's troubles were related to the overwhelming set of variables—along with something else. His checkerboard array of data was too coarse in both space and time. He needed more data points and needed to perform many, many more calculations to even approximate tomorrow's weather. He wasn't aware of that problem back in the World War I era. After all, he did spend the better part of a year trying to get one 24 hour forecast together. How many more calculations could he reasonably be expected to make? We have to cut him some slack—he and his assistants were only human.
But that was the problem—they were only human and could perform only a modest number of calculations. A mathematical instability set into his experiment, and the entire effort blew up. Let me give you an example of this computational instability.
Suppose you live in Chicago, and the wind is coming from Peoria, a little more than 100 miles away. The temperature in Chicago is 70 degrees, and in Peoria, the thermometer reads 80. That's a 10-degree difference in 100 miles. If the wind is blowing at 20 mph, it might be projected that in five hours the temperature will rise those 10 degrees. That rate of change of temperature is 2 degrees per hour. If you use that rate of change beyond five hours, let's say for 20 hours, you might predict that in 20 hours the temperature will go up a full 40 degrees, to 110 degrees! That's ludicrous, but that's the problem you run into if you make calculations over too large a time interval across a too sparsely defined array of data points.
Through the 1920s and 1930s, nothing could be done to solve this problem. But by the 1940s, a new era was born. The computer arrived.
A Brief History of the Computer
The first widely used commercial electronic computer was the famous UNIVAC (Universal Variable Computer). CBS television was one of the first organizations to use it. The network wanted it to predict the outcome of the 1952 presidential election. UNIVAC's first prediction of a landslide was right on the money, but the human operators of the machine did not believe the results. So they reprogrammed it—then it incorrectly predicted a close election. The operators tampered with success, and UNIVAC's revised forecast was way off. This story underscores the reluctant acceptance of computer products, especially in the early days.
Weather-Speak
UNIVAC, or Universal Variable Computer, was built in 1951 and was the first commercially available electronic computer. It stored data on magnetic tape. UNIVACs were sold for about one million dollars each.
The vacuum tube made computers possible in the 1940s. As early as the seventeenth century, Blaise Pascal invented a machine with gears that could add and subtract. Later, in the nineteenth century, British scientist Charles Babbage came up with the concept of a complex mechanical device called the analytical engine. It was designed so that it could perform mathematical manipulations from a set of instructions that were read into it on perforated cards. Still, this device, as visionary as it may seem, could never be completed because of all the mechanisms involved with the operation—just too many moving parts.
That changed in the twentieth century, when vacuum tubes came along and were able to generate electronics in place of the mechanical gears and wheels. During the 1940s, a series of electronic computers were put together. The need for new technology during World War II helped spur the computer development along. One early version known as ENIAC (electronic numerical integrator and computer) was finished in early 1945. This computer contained 18,000 vacuum tubes. The energy drawn by all the tubes in early computers caused lights to dim in nearby communities. At the same time, the computers generated tremendous amounts of heat, which required ventilation, occupied large rooms, and frequently failed. During the late 1940s, transistor technology solved some of the problems, and after the computer chip was developed in the 1960s, there was no stopping these machines. Desktop home computers of the 1990s have more memory, speed, and power than the grand mainframe computers of the 1950s and 1960s.

Excerpted from The Complete Idiot's Guide to Weather © 2002 by Mel Goldstein, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.







