Geometry: Isometries

Isometries

The word isometry is used to describe the process of moving a geometric object from one place to another without changing its size or shape. Imagine two ants sitting on a triangle while you move it from one location to another. The location of the ants will change relative to the plane (because they are on the triangle and the triangle has moved). But the location of the ants relative to each other has not. Whenever you transform a geometric figure so that the relative distance between any two points has not changed, that transformation is called an isometry. There are many ways to move two-dimensional figures around a plane, but there are only four types of isometries possible: translation, reflection, rotation, and glide reflection. These transformations are also known as rigid motion. The four types of rigid motion (translation, reflection, rotation, and glide reflection) are called the basic rigid motions in the plane. These will be discussed in more detail as the section progresses.

An isometry in the plane moves each point from its starting position P to an ending position P´, called the image of P. It is possible for a point to end up where it started. In this case P = P´ and P is called a fixed point of the isometry. In studying isometries, the only things that are important are the starting and ending positions. It doesn't matter what happens in between.

Consider the following example: suppose you have a quarter sitting on your dresser. In the morning you pick it up and put it in your pocket. You go to school, hang out at the mall, flip it to see who gets the ball first in a game of touch football, return home exhausted and put it back on your dresser. Although your quarter has had the adventure of a lifetime, the net result is not very impressive; it started its day on the dresser and ended its day on the dresser. Oh sure, it might have ended up in a different place on the dresser, and it might be heads up instead of tails up, but other than those minor differences it's not much better off than it was at the beginning of the day. From the quarter's perspective there was an easier way to end up where it did. The same effect could have been accomplished by moving the quarter to its new position first thing in the morning. Then it could have had the whole day to sit on the dresser and contemplate life, the universe, and everything.

If two isometries have the same net effect they are considered to be equivalent isometries. With isometries, the “ends” are all that matters, the “means” don't mean a thing.

An isometry can't change a geometric figure too much. An isometry will not change the size or shape of a figure. I can phrase this in more precise mathematical language. The image of an object under an isometry is a congruent object. An isometry will not affect collinearity of points, nor will it affect relative position of points. In other words, if three points are collinear before an isometry is applied, they will be collinear afterwards as well. The same holds for between-ness. If a point is between two other points before an isometry is applied, it will remain between the two other points afterward. If a property doesn't change during a transformation, that property is said to be invariant. Collinearity and between-ness are invariant under an isometry. Angle measure is also invariant under an isometry.

If you have two congruent triangles situated in the same plane, it turns out that there exists an isometry (or sequence of isometries) that transforms one triangle into the other. So all congruent triangles stem from one triangle and the isometries that move it around in the plane.

You might be tempted to think that in order to understand the effects of an isometry on a figure, you would need to know where every point in the figure is moved. That would be too complicated. It turns out that you only need to know where a few points go in order to know where all of the points go. How many points is “a few” depends on the type of motion. With translations, for example, you only need to know the initial and final positions of one point. That's because where one point goes, the rest follow, so to speak. With isometries, the distance between points has to stay the same, so they are all kind of stuck together.

Because you will be focusing on the starting and ending locations of points, it is best to couch this discussion in the Cartesian Coordinate System. That's because the Cartesian Coordinate System makes it easy to keep track of the location of points in the plane.

Translations

When you translate an object in the plane, you slide it around. A translation in the plane is an isometry that moves every point in the plane a fixed distance in a fixed direction. You don't flip it, turn it, twist it, or bop it. In fact, with translations if you know where one point goes you know where they all go.

The simplest translation is the “do nothing” translation. This is often referred to as the identity transformation, and is denoted I. Your figure ends up where it started. All points end up where they started, so all points are fixed points. The identity translation is the only translation with fixed points. With every other translation, if you move one point, you've moved them all. Figure 25.1 shows the translation of a triangle.

Figure 25.1The translation of a triangle.

Translations preserve orientation: Left stays left, right stays right, top stays top and bottom stays bottom. Isometries that preserve orientations are called proper isometries.

Reflections

A reflection in the plane moves an object into a new position that is a mirror image of the original position. The mirror is a line, called the axis of reflection. If you know the axis of reflection, you know everything there is to know about the isometry.

Reflections are tricky because the frame of reference changes. Left can become right and top can become bottom, depending on the axis of reflection. The orientation changes in a reflection:

Clockwise becomes counterclockwise, and vice versa. Because reflections change the orientation, they are called improper isometries. It is easy to become disorientated by a reflection, as anyone who has wandered through a house of mirrors can attest to. Figure 25.2 shows the reflection of a triangle.

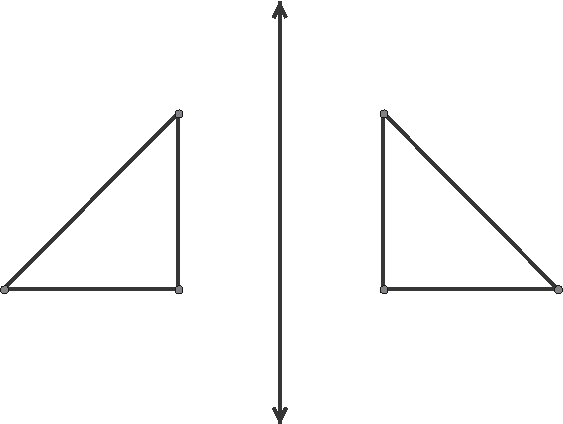
Figure 25.2The reflection of a right triangle.

There is no identity reflection. In other words, there is no reflection that leaves every point on the plane unchanged. Notice that in a reflection all points on the axis of reflection do not move. That's where the fixed points are. There are several options regarding the number of fixed points. There can be no fixed points, a few (any finite number) fixed points, or infinitely many fixed points. It all depends on the object being reflected and the location of the axis of reflection. Figure 25.3 shows the reflection of several geometric figures. In the first figure, there are no fixed points. In the second figure there are two fixed points, and in the third figure there are infinitely many fixed points.

Figure 25.3A reflected object having no fixed points, two fixed points, and infinitely many fixed points.

A reflection can be described by how it changes a point P that is not on the axis of reflection. If you have a point P and the axis of reflection, construct a line l perpendicular to the axis of reflection that passes through P. Call the point of intersection of the two perpendicular lines M. Construct a circle centered at M which passes through P. This circle will intersect l at another point beside P, say P´. That new point is where P is moved by the reflection. Notice that this reflection will also move P´ over to P.

That's just half of what you can do. If you have a point P and you know the point P´ where the reflection moves P to, then you can find the axis of reflection. The preceding construction discussion gives it away. The axis of reflection is just the perpendicular bisector of the line segment ¯PP´! And you know all about constructing perpendicular bisectors.

What happens when you reflect an object twice across the same axis of reflection? The constructions discussed above should shed some light on this matter. If P and P´ switch places, and then switch places again, everything is back to square one. To the untrained eye, nothing has changed. This is the identity transformation I that was mentioned with translations. So even though there is no reflection identity per se, if you reflect twice about the same axis of reflection you have generated the identity transformation.

Rotations

A rotation involves an isometry that keeps one point fixed and moves all other points a certain angle relative to the fixed point. In order to describe a rotation, you have to know the pivot point, called the center of the rotation. You also have to know the amount of rotation. This is specified by an angle and a direction. For example, you could rotate a figure about a point P by an angle of 90º, but you need to know if the rotation is clockwise or counterclockwise. Figure 25.4 shows some examples of rotations about some points.

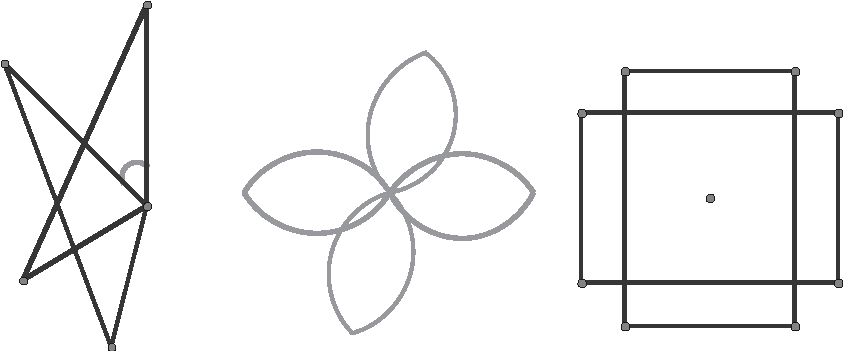
Figure 25.4Examples of rotations of figures.

Other than the identity rotation, rotations have one fixed point: the center of rotation. If you turn a point around, you don't change it, because it has no size to speak of. Also, a rotation preserves orientation. Everything rotates by the same angle, in the same direction, so left stays left and right stays right. Rotations are proper isometries. Because rotations are proper isometries and reflections are improper isometries, a rotation can never be equivalent to a reflection.

In order to describe a rotation, you need to specify more information than one point's origin and destination. Infinitely many rotations, each with a distinct center of rotation, will take a specific point P to its final location P´. All of these different rotations have something in common. The centers of rotation are all on the perpendicular bisector of the line segment ¯PP´. In order to nail down the description of a rotation, you need to know how two points change, but not just any two points. The perpendicular bisectors of the line segments connecting the initial and final locations of the points must be distinct. Suppose you know that P moves to P´ and Q moves to Q´ , with the perpendicular bisector of ¯PP´ distinct from the perpendicular bisector of ¯QQ´. Then the rotation is specified completely. Figure 25.5 will help you visualize what I am trying to describe.

The center of rotation must lie on the perpendicular bisectors of both ¯PP´ and ¯QQ´ , and you know that two distinct nonparallel lines intersect at a point. The point of intersection of the perpendicular bisectors will be the center of rotation, C. To find the angle of rotation, just find m∠PCP´.

Figure 25.5A rotation with center of rotation point C and angle of rotation m∠PCP´.

Glide Reflections

A glide reflection consists of a translation followed by a reflection. The axis of reflection must be parallel to the direction of the translation. Figure 25.6 shows a figure transformed by a glide reflection. Notice that the direction of translation and the axis of reflection are parallel.

Notice that the orientation has changed. If you list the vertices of the triangle clockwise, the order is A, B, and C. If you list the vertices of the resulting triangle clockwise, the order is A´ , C´ , and B´. Because the orientation has changed, glide reflections are improper isometries.

In order to understand the effects of a glide reflection you need more information than where just one point ends up. Just as you saw with rotation, you need to know where two points end up. Because the translation and the axis of reflection are parallel, it is easy to determine the axis of reflection when you know how two points are moved. If P is moved to P´ and Q is moved to Q´, the axis of reflection is the line segment that connects the midpoints of the segments ¯PP´ and ¯QQ´. When the axis of reflection is known, you need to reflect the point P´ across the axis of reflection. That will give you an intermediate point P*. The translation part of the glide reflection (in other words, the glide part) is the translation that moved P to P*. Now you know the translation and the axis of reflection, so you know everything about the isometry.

Because a glide reflection is a translation and a reflection, it will have no fixed points (assuming the translation is not the identity!). That's because nontrivial translations have no fixed points.

Figure 25.6ΔABC undergoes a glide reflection.