Compound Inequalities
Compound Inequalities
You can define a range of values using a single inequality statement, called a compound inequality. Rather than say that, for a given equation, x > 2 and also x ¤ 9, you could write 2 x x, which is less than or equal to 9," but you might understand it better if I reword it like this: "x has a value between 2 and 9it might even be 9, but it can't be 2."
Talk the Talk
A compound inequality is a single statement used to represent two inequalities at once, such as a x b. It describes a range (or interval) of numbers, whose lower boundary is a, and whose upper boundary is b. Whether or not those numbers are actually included in the interval is decided by the attached inequality sign. If the symbol is ¤, then the number is included; if it's
In Figure 7.3, I illustrate the parts of a compound inequality. Notice that you should always write the lower boundary on the left and the upper boundary on the right. Furthermore, you should always use either the

Figure 7.3
Solving Compound Inequalities
Notice that a compound inequality has three pieces to it, rather than the usual two sides of an equation or simple inequality. In order to solve a compound inequality, your job is to isolate the variable in the middle of the statement. Do this by adding, subtracting, multiplying, and dividing the same thing to all three parts of the inequality at the same time.
Kelley's Cautions
If you have to divide all three parts of a compound inequality by a negative number, you'll have to reverse both inequality signs to end up with this: b > x > a, where b is the upper boundary and a is the lower boundary. That's okay, but I prefer it rewritten as a x b, with less than signs and the lower boundary back on the left, where it belongs.
Example 4: Solve the inequality - 4 ¤ 3x + 2
Solution: You want to isolate the x where the 3x +2 now is, so start by subtracting 2, not only from there, but from all three parts of the inequality.
- -6 ¤ 3x
To eliminate the x's coefficient, divide everything by 3.
- -2 ¤ x
This means any number between -2 and 6 (including -2 but excluding 6) will make the compound inequality true.
You've Got Problems
Problem 4: Solve the inequality -1 x + 5
Graphing Compound Inequalities
To graph a compound inequality, use dots to mark its endpoints on a number line. Just like in basic inequality graphs, the dots of compound inequalities correspond with the type of inequality symbol. Specifically, the symbol ¤ should be marked with a solid dot, and the symbol
Once you've drawn the dots, draw a dark segment connecting them. This dark segment indicates that all the numbers between the endpoints are solutions to the inequality.
Example 5: Graph the compound inequality -14 x ¤ -6.
Solution: Since -14, the lower endpoint of this interval, has a
You've Got Problems
Problem 5: Graph the compound inequality -2 ¤ x
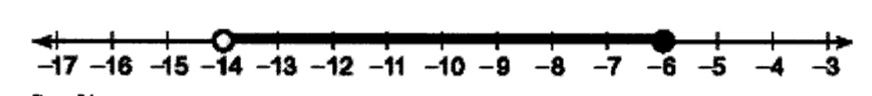
Figure 7.4The graph of -14

Excerpted from The Complete Idiot's Guide to Algebra © 2004 by W. Michael Kelley. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
You can also purchase this book at Amazon.com and Barnes & Noble.







