Algebra: Tricky Linear Equations
Tricky Linear Equations
For the rest of the section, I want to focus on the skill of designing linear equations when you're not given an explicit slope. You're still going to use the point-slope form to write the equation, it's just that you'll have to figure out the slope first. Finding the slope won't be hard, but the method you use to find it will vary based on what sort of information is given in the problem.
Essentially, you'll be faced with two kinds of tricky linear equation problems, one in which you're given two points on the line and asked to create the equation, and one in which you have to create a line either perpendicular or parallel to a second line.
How to Get from Point A to Point B
One classic type of algebra problem asks you to write the equation of a line that passes through two points. Back in Graphing Linear Equations, you calculated the slope of such a line using something I creatively called the "slope formula." In case you forgot that formula, it said that a line passing through points (a,b) and (c,d) has the following slope:
- m = d - bc - a
Now it's time to put that formula to good use. Not only will you find the slope of the line passing through a couple of points, you'll find the equation of that line as well.
Example 5: Write the equation of the line that passes through the points (-4,7) and (2,-1) in standard form.
Solution: Remember, to create a linear equation, you need the slope of the line and one point on the line. You're actually given two points on the line for this problem, but you still need the slope, which is calculated with the slope formula like so:
- m = -1 -(7)2 - (-4)
- m = -86
- m = - 43
Now that you have the slope, pick one of the two points you're given and apply the point-slope form. Here's what that substitution looks like if you choose the point (2,-1):
- y - y1 = m(x - x1)
- y -(-1) = -43(x - (2))
- y + 1 = -43x + 83
The problem does ask you to put this in standard form, so eliminate those fractions by multiplying everything by 3.
- 3(y + 3)= -4x + 8
Rearrange the terms to comply with the requirements of standard form.
- 4x + 3y = 5
Critical Point
Once you figure out the slope in Example 5, it doesn't matter which point you use in point-slope formeither one will result in an equivalent equation. In case you need to see it to believe it, here's what the work looks like if you choose the point (-4,7) instead of (2,-1):
y - y1 = m(x - x1)
y - (7) = -43x - 163
3(y - 7) = 31(-43x - 163)
3y - 21 = -4x - 16
4x + 3y = 5
Pretty cool, eh? The final answers are the same.
Here's a tip: You can check your answer by plugging both of the original points into the equation you got. If they each result in true statements, you did everything right:
| Check (-4,7) | Check (2,-1) |
|---|---|
| 4(-4) + 3(7) = 5 | 4(2) + 3(-1) = 5 |
| -16 + 21 = 5 | 8 - 3 = 5 |
| 5=5 | 5=5 |
You've Got Problems
Problem 5: Write the equation of the line that passes through the points (-3,5) and (-8,0) in standard form.
Parallel and Perpendicular Lines
You may not know a lot about geometry yet, and that's okay. (By the way, the technical definition of geometry, according to Webster's Dictionary, is "What an acorn says when it grows up." Get it? "Gee-I'm-a-tree?") However, you may be asked to construct equations of parallel and perpendicular lines in algebra, so here's a basic explanation of those concepts:
- Parallel lines never intersect one another. Like railroad tracks, they run on and on but never touch one another. This is due to the fact that parallel lines have the same exact slope, which keeps the lines the same exact distance from one another forever and ever.
- Perpendicular lines intersect one another at right, or 90-degree, angles. If that doesn't make sense, think of it this way: If planted in a flat plot of land, a tree will grow perpendicular to the ground. Perpendicular lines have slopes which are opposite reciprocals of one another.
Critical Point
Parallel lines do not intersect because they have the same slope. However, perpendicular lines meet at 90-degree angles, thanks to slopes which are opposite reciprocals. In other words, if lines l and n are perpendicular and the slope of line l is ab, then the slope of n would be -ba.
In Figure 6.2, I've graphed a set of parallel lines and a set of perpendicular lines and indicated their slopes. In case you're wondering where I got the slope values, I have also highlighted points on the lines; if you want to generate the slopes for yourself, just plug their coordinates into the slope formula.
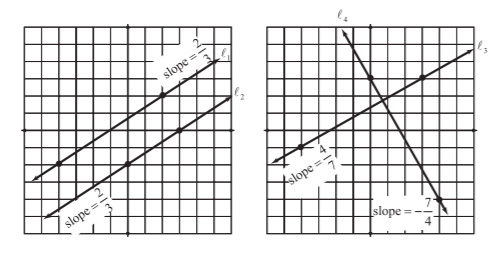
Figure 6.2Lines l1 and l2 are parallel, because they have the same slope. On the other hand, the slopes of the perpendicular lines are opposite reciprocals of one another.
Example 6: Write the equation of line k in slope-intercept form if it passes through the point (2,-3) and is perpendicular to the line with equation x - 5y = 7.
Solution: You already know a point on k, so basically all you need is the slope of k in order to create its equation. You do know that k will be perpendicular to the line x - 5y = 7, so put that line in slope-intercept form to figure out what its slope is. In other words, solve x - 5y = 7 for y:
- y = 15x - 75
This line has slope 15. Therefore, line k's slope will be the opposite reciprocal of 15, which is -51 = -5 ; just flip the fraction upside down and multiply it by -1.
You've Got Problems
Problem 6: Write the equation of line j in standard form if j passes through the point (-6,1) and is parallel to the line -2x + 6y = 7.
Now that you have the slope of k and one of its points, apply the point-slope form.
- y - (-3) = -5(x - (2))
- y + 3 = -5x + 10
Since the problem asks for the answer in slope-intercept form, solve for y.
- y = -5x + 7

Excerpted from The Complete Idiot's Guide to Algebra © 2004 by W. Michael Kelley. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
You can purchase this book at Amazon.com and Barnes & Noble.







