Chemistry: A Quantum Leap into Quantum Mechanics

A Quantum Leap into Quantum Mechanics

Unfortunately for Bohr, his model didn't properly explain how atoms behave. Fortunately, quantum mechanics came to the rescue!

What Do Orbitals Look Like?

The Bohr model was definitely a step in the right direction. After all, if the model could be used to predict the orbital energies of hydrogen, there must be something to it! Unfortunately, there was one small problem: it was ineffective at predicting the orbital energies of any other element. As a result, the hunt to come up with something more effective was on.

After a whole lot of work by a whole lot of really famous guys you've probably never heard of, a new model of the atom was born. This new model, called quantum mechanics, sums up our current understanding of how atoms work.

The problem with Bohr's model was that there weren't enough variables in his equation to do a good job of predicting the orbital energies of elements other than hydrogen. Eventually, the Schrdinger equation was written to explain these orbital energies.

When the Schrdinger equation was put together, a really strange thing happened. Whereas previous models of the atom had predicted that electrons were particles that zoomed around in predictable paths, the Schrdinger equation predicted that it was possible to predict where electrons would probably be found, but impossible to predict exactly where you could find them. However, you can express the probability of finding an electron with a mathematical function called a wavefunction. As a result, orbitals went from being two-dimensional circular orbits to 3-D shapes, some of them very weird.

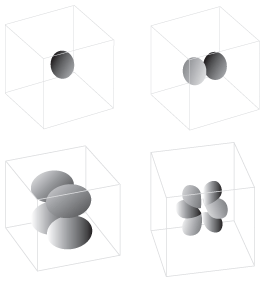
Figure 5.4These diagrams represent the four types of atomic orbitals.

You may be wondering how somebody just learning about quantum mechanics can understand how wavefunctions work. Since differential equations are really hard, learning the Schrdinger equation directly isn't practical for most of us. Instead, we'll get a little help from our friendly neighborhood garden sprinkler.

Imagine that you've just turned on a sprinkler and are watering your lawn. Most of the water that leaves the sprinkler head lands pretty close to the sprinkler itself, and as you move away from the sprinkler, fewer and fewer drops hit any one location. If you wanted to measure exactly how much water lands at any location, you could set out little rain gauges all over your lawn. Let's make a chart that shows what these rain gauges would look like.

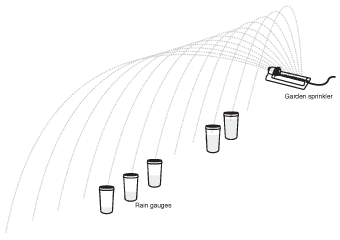
Figure 5.5By placing rain gauges near a lawn sprinkler, we get an idea of where future raindrops might land. This type of chart is referred to as a "probability distribution."

Now for a couple of difficult questions:

1. What is the maximum distance that a drop can land from the sprinkler? This is a tough one. There isn't any limit to how far a drop can go—in fact, if you've ever stood near a sprinkler, you can see that a few stray water drops always land outside the area that really gets a good dousing. So, what's the maximum distance? There isn't one!
2. If you were to inject a single drop of colored water into the hose, where would it land? From the accompanying figure we can see that it will probably land near the sprinkler, but there's also a chance that it will land farther away. Unfortunately, our diagram doesn't tell us for sure where the drop will land, though it does tell us the probability of finding a drop at any one location.

The garden sprinkler figure is referred to as a "probability distribution" because it gives us an idea of where we're likely to see the water drops fall. In the same way, we can draw a probability distribution that gives us an idea of where we're likely to find an electron in an atom. Just like the sprinkler example, we can't know from this chart where an electron will be. It does, however, give us some idea as to where we'll find it.

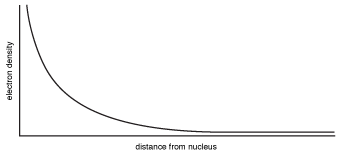
Figure 5.6From this diagram, you can see that electrons can be compared to the individual water drops from a lawn sprinkler. You can never tell exactly where they'll land, but the probability distribution tells you where they're most likely to be found.

If we sketch these probabilities out on paper, we can see that s-orbitals have a spherical shape, with the electrons most likely to be found near the center and less likely to be found near the edges. The sketch shown in the following figure is what an s-orbital looks like.

Figure 5.7Though s-orbitals are spherical with a fuzz of decreasing probability near the edges, they're usually just drawn as spheres to make them easier to visualize.

Where Do These Fancy Orbital Shapes Come From?

A few pages ago we mentioned that the equations that describe electrons are a lot fancier in quantum mechanics than they are in the Bohr model. To make these equations work, four variables called quantum numbers are needed, rather than the one variable (n) that Bohr used.

• The principal quantum number, n. This is the same n that Bohr used, and is used to describe the energy level of an electron. The allowed values for n are 1, 2, 3, … to infinity.
• The angular momentum quantum number, l. This quantum number is used to determine the shape and type of the orbital. Possible values for l are 0, 1, 2, and so on up to (n-1). For example, if n=2, the possible values for l are 0 and 1. A spherical s-orbital is defined as l=0, a dumbbell-shaped p-orbital is defined as l=1, an oddly shaped d-orbital is defined as l=2, and a really weird f-orbital is defined as l=3.

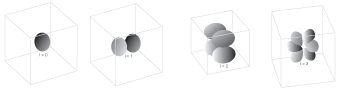
Figure 5.8The value of l determines the shape and type of orbital being described.

• The magnetic quantum number, m_l. The magnetic quantum number determines the direction that the orbital points in space. Possible values for m_l are all the integers from -l through l. For example, if l=2, the possible values of m_l are -2, -1, 0, 1, 2. Because p-orbitals are denoted by l=1, there are three possible directions that they can point, denoted by m_l = -1, 0, 1. These three directions lie along the x-, y-, and z-axes (see accompanying figure).

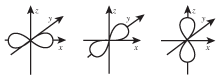
Figure 5.9These three p-orbitals are referred to as being "degenerate," because they have exactly the same energy.

• Similarly, there is one s-orbital per energy level—since l=0, the only value for m_l = 0. There are also five d-orbitals per energy level (l=2, so m_l = -2, -1, 0, 1, 2) and seven f-orbitals (l=3, so m_l = -3, -2, -1, 0, 1, 2, 3).

• The spin quantum number, m_s. Possible values for m_s are +¹⁄₂ and -¹⁄₂. The reason we need a spin quantum number comes from the Pauli exclusion principle, which states that no two electrons in an atom can have the same set of quantum numbers. Now, if we only had the quantum numbers n, l, and m_l, the Pauli exclusion principle would force each electron to be in its ownorbital. Because it's well known that orbitals are is described by an electron with capable of holding two electrons, we need to define a fourth quantum number that allows us to distinguish between them.

Electron Configurations (the Long Way)

So far, we've talked about the nature of orbitals with the quantum model and the variables that define their shapes. What we haven't yet discussed is where the electrons for particular elements can be found.

Before we can understand how electrons occupy the orbitals in an atom, we need to learn which orbitals have the lowest energies and which have the highest energies. After all, electrons will fill up low-energy orbitals before they start to fill high energy orbitals, so if we can order the orbitals by increasing energy, we can determine where all of the electrons in an atom go.

In each principal energy level, s-orbitals have the lowest energies, followed by p-orbitals, d-orbitals, and f-orbitals (which have the highest energies). As a result, electrons will go to s-orbitals before entering p-orbitals and so on for d- and f-orbitals.

Once we know where all the electrons in an atom belong, we can write electron configurations for the atom. An electron configuration is nothing more than a list of orbitals that contain the electrons in an atom. Electron configurations usually contain many terms, each of which have the general format:

• n (type of orbital)^{number of electrons in that type of orbital}

Memorizing the electron configurations of each element is possible, but not much fun. Instead, we'll use the periodic table to help us with our task. To make life really easy, we'll label our periodic table in a way that gives us the most possible useful information about electron configurations.

Let's look at some examples:

• Hydrogen has only one electron. Hydrogen is in the first row of the periodic table, making the principal quantum number 1. The type of orbital the ground state electron lies in (shown by the color of the element on this handy card) is an s-orbital. As a result, the electron configuration for hydrogen is said to be 1s¹, where the one in front stands for the principal quantum number and the one after the "s" stands for the number of electrons in that orbital.
• Helium has two electrons. Since helium is also in the first row of the periodic table, n is still equal to 1. Helium is in the s-region of the periodic table, meaning that the electrons are in the 1s orbital. As a result, helium's electron configuration is 1s².
• Lithium has three electrons. The first two electrons are the same as those in helium. So the first term will be 1s². The third electron is represented by lithium's position on the periodic table, which is in the second energy level and in the s-region of the periodic table, making the second term 2s¹. Putting them together, the electron configuration is said to be 1s²2s¹.

• Beryllium has four electrons. The first two are the same as helium (making the first term 1s²) and the second two are in the 2s orbital (making the second term 2s²). Overall, the electron configuration is 1s²2s².
• Boron has five electrons. The first two are the same as those in helium (making the first term 1s²) and the second two are the same as beryllium (making the second term 2s²). The fifth electron is represented by boron's position on the periodic table, which is in the second row and p-section of the table. The third term, then, is 2p1, making the overall electron configuration 1s²2s²2p¹.
• In the same way, the electron configuration for carbon's six electrons is 1s²2s²2p², and the electron configuration for nitrogen's seven electrons is 1s²2s²2p³.

There are only a few variations from this pattern that we can see. Let's use scandium (Sc) as an example. You might think that the electron configuration would be 1s²2s²2p⁶3s²3p⁶4s²4d¹, which isn't a bad guess based on what we've seen earlier. However, something very important to remember is that the number in front of the d-orbitals is always one behind the energy level of the s-orbitals. As a result, it's not a 4d orbital, it's a 3d orbital. The correct electron configuration, then, is 1s²2s²2p⁶3s²3p⁶4s²3d¹.

In the same vein, the f-orbitals also cause some trouble when doing electron configurations. Instead of having the same n value as the s-orbitals, f-orbitals are two behind. As a result, cerium (Ce) has an electron in the 4f orbitals, not the 6f orbitals.

For those of you who want to see how the whole thing plays out, we'll use the example of lead (Pb). The complete electron configuration for lead is 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p⁶6s²4f¹⁴5d¹⁰6p².

Electron Configurations (the Short Way)

Now that you know how to write electron configurations the long way, we can concentrate on doing it in a much less tedious fashion. For those of you who skipped the long version to see what the short way was, go back and learn the long way or you won't have any idea what we're talking about in this section.

As you've undoubtedly been able to tell, electron configurations involve a lot of repetition. Every element from helium on has the "1s2" term. As a result, it's usually not handy to write out every single term for every element. Instead, what we'll do is write only the last few terms for each element, starting instead at the previous noble gas (they're the elements in the far right column of the periodic table—we discuss them. To denote that you've done this, write the symbol of the noble gas in [brackets].

Example: The electron configuration of phosphorus (P) can be written in shorthand as [Ne] 3s²3p³. Isn't that nicer than writing out all those other terms? Similarly, you can abbreviate something as obnoxious as plutonium (Pu) as [Rn] 7s²5f⁶, a great improvement over the old method.

Orbital Filling Diagrams and Hund's Rule

When I get on the bus I don't like to sit next to other people if I can avoid it. Though somebody may look okay when I first sit next to them, invariably they start picking their nose or sneezing on me or eating a meatball sandwich as soon as I get comfortable. Over the years, I've learned that I'd better head for empty seats if it's at all possible. I've noticed that I'm not the only person to act this way—most people do the same thing.

Electrons work in the same way. Let's consider the case of carbon, which has the electron configuration 1s²2s²2p². Since there is only one s-orbital per energy level, the electrons in the 1s and 2s orbitals are stuck pairing up. However, since there are three p-orbitals per energy level, the two electrons in the 2p orbitals will choose to go into different p-orbitals rather than sticking around together. If we were to sketch this, with low-energy orbitals being further down on the diagram than higher-energy orbitals, we'd see the following:

Figure 5.11The orbital filling diagram for carbon.

The fact that electrons will want to stay unpaired whenever possible in orbitals with equal energies is called Hund's rule. Hund's rule states that electrons will stay unpaired whenever possible in orbitals with equal energies.

Of course, if we add enough electrons, we get into a situation where we simply have to start putting two electrons together in the same orbital. An example of this can be found with oxygen, which has the electron configuration 1s²2s²2p⁴.

As you can see, the four electrons in the 2p orbital have been forced to pair up. However, since we have four electrons and three orbitals, Problem 4: Draw the orbital fill-only one of the orbitals needs to contain paired-ing diagram for chlorine. up electrons. We see the same situation happening with other elements as well.