Geometry: Parallel Lines and Supplementary Angles
Parallel Lines and Supplementary Angles
Whenever two parallel lines are cut by a transversal, an interesting relationship exists between the two interior angles on the same side of the transversal. These two interior angles are supplementary angles. A similar claim can be made for the pair of exterior angles on the same side of the transversal. There are two theorems to state and prove. I'll give formal statements for both theorems, and write out the formal proof for the first. The second theorem will provide yet another opportunity for you to polish your formal proof writing skills.
- Theorem 10.4: If two parallel lines are cut by a transversal, then the interior angles on the same side of the transversal are supplementary angles.
- Theorem 10.5: If two parallel lines are cut by a transversal, then the exterior angles on the same side of the transversal are supplementary angles.
Let the fun begin. As promised, I will show you how to prove Theorem 10.4.
Figure 10.6 illustrates the ideas involved in proving this theorem. You have two parallel lines, l and m, cut by a transversal t. You will be focusing on interior angles on the same side of the transversal: ∠2 and ∠3. You'll need to relate to one of these angles using one of the following: corresponding angles, vertical angles, or alternate interior angles. There are many different approaches to this problem. Because Theorem 10.2 is fresh in your mind, I will work with ∠1 and ∠3, which together form a pair ofalternate interior angles.
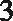
Figure 10.6l m cut by a transversal t.
- Given: l m cut by a transversal t.
- Prove: ∠2 and ∠3 are supplementary angles.
- Proof: You will need to use the definition of supplementary angles, and you'll use Theorem 10.2: When two parallel lines are cut by a transversal, the alternate interior angles are congruent. That should be enough to complete the proof.
| Statements | Reasons | |
|---|---|---|
| 1. | l m cut by a transversal t | Given |
| 2. | ∠2 and ∠3 are same-side interior angles | Definition of same-side interior angles |
| 3. | ∠1 and ∠3 are alternate interior angles | Definition of alternate interior angles |
| 4. | ∠1 and ∠2 are supplementary angles, and m∠1 + m∠2 = 180º | Definition of supplementary angles |
| 5. | ∠1 ~= ∠3 | Theorem 10.2 |
| 6. | m∠1 = m∠3 | Definition of ~= |
| 7. | m∠13 + m∠2 = 180º | Substitution (steps 4 and 6) |
| 8. | ∠2 and ∠3 are supplementary angles | Definition of supplementary angles |
Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







