Completing the Square
Completing the Square
The next technique you can use to solve quadratic equations is called completing the square; it forces the equation, against its will, to contain a perfect square, which can then be easily eliminated.
Completing the square isn't exactly the easiest way to solve quadratic equations; its strength lies in the fact that the process is repetitive and predictable. It's like that guy you knew in high school whose parents made him take his cousin (who usually looks like a perfect square) to the prom. Sure it was awkward, and neither of them really had a lot of fun, but at least their parents knew exactly how the evening was going to end. (After all, this was his cousin, so there was no prospect of post-dance "extracurricular activities.")
Here's the best news yet: Completing the square will always work, unlike the factoring method, which, of course, requires that the trinomial be factorable.
However, you need to learn one thing before I can show you how to complete the square: how to eliminate exponents in equations.
Solving Basic Exponential Equations
Last section you learned how to solve radical equations. During that process, you found out raising both sides of an equation to the nth power cancels out a radical with index n. In other words, to solve the equation
you would have to raise both sides of the equation to the fourth power, leaving you with
- x - 1 = 81
- x = 82
This process also works in reverse. In other words, you can cancel out an exponent of n by taking the nth root of both sides of the equation. For example, to solve the equation
- 5x3 = 80
you'd first isolate the quantity raised to the exponent (just like you did in radical equations).
- x3 = 16
To cancel out the exponent of 3, leaving behind only what was once raised to the third power, take the third root of both sides of the equation.
- x = 232
You've Got Problems
Remember, last section you learned that nxn when n is an even number. The "±" rule discussed here takes care of that for you when dealing with equations.
There's only one major thing to keep in mind when canceling out that exponent: If you're canceling out an even exponent, you need to stick in a "±" sign on the left side of the equation when you jam those radical signs on.
For example, consider the equation x2 = 16. You can solve for x by square rooting both sides of the equation.
- x2 = ± 16
- x = ±4
Bugging Out with Squares
Now it's finally time to date your cousin, er, complete the square. Because there are a lot of steps involved, I should explain how they work in the context of an example. Just a brief warning before I get started: This problem will contain a scatological reference and is hence rated PG by the National Advisory Council on Lowbrow Humor in Mathematics.
Example 2: Solve the equation 2x2 - 16x + 10 = 0.
Solution: Even though you can factor out a GCF of 2, the resulting equation, 2(x2 - 8x + 5) = 0, cannot be factored further. So in order to solve it, you have to resort to completing the square.
Step 1: Make sure the coefficient of x2 is 1. If it's not, divide everything in the equation by that coefficient. In this problem, the coefficient of x2 is 2, so divide everything by 2.
- x2 - 8x + 5 = 0
Talk the Talk
If you forget to make the coefficient of x2 equal to 1, you'll get stuck later on, in Step 4.
Step 2: Move everything to the left side of the equation except the constant. You want that constant sitting alone on the right side of the equation. In this example, that means subtracting 5 from both sides.
- x2 - 8x = -5
Step 3: Inspect bug droppings. This is the key step for completing the square: You're going to add a mystery number to both sides of the equation. To find that number, take half of the x coefficient (half of -8 is -4) and square it ((-4)2 = 16). So, in this case, the mystery number to be added to both sides of the equation is 16.
I don't know when, why, or how I came up with it, but for years I have used a little, three-segmented bug (pictured in Figure 13.1.) to help me remember this step. To this day, I still draw his body (minus the legs, eyes, and other time-consuming details) in the margins of a completing the square problem.
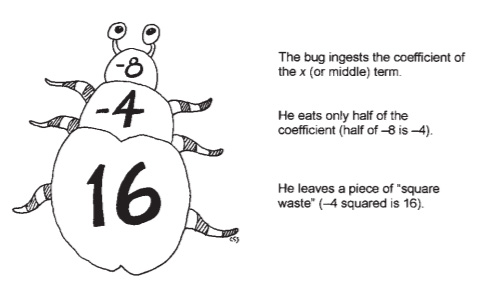
Figure 13.1Don't turn on a bright light while working with the bug, or he may scuttle under the fridge.
Here's how my little invertebrate mnemonic friend works: The bug eats the x coefficient (place the x coefficient, including its sign, in the top segment); however, he's only a bug with a small appetite, so he is only able to eat half of that number (put half of the number located in the first segment, including its sign, in the second segment). Finally, once that number's eaten, he must, ahem, excrete some waste to complete the digestive process, and this bug only leaves square droppings (the square of the middle segment is written in the bug's rear end).
Talk the Talk
This procedure is called completing the square because, by adding 16 to both sides in Example 2, you're creating a trinomial that's a perfect square. Therefore, it can be written as (x + a)2, where a is the number from the bug's midsection.
Whether you choose to use the bug to generate the mystery number or not, you should add it (it will always be positive since it is the result of a square) to both sides of the equation.
- x2 - 8x + 16 = -5 + 16
- x2 - 8x + 16 = 11
Step 4: Rewrite the left side of the equation as a perfect binomial square. When factored, the quadratic on the left side will look like this: (x + a)2. Here's the cool part: The a in (x + a)2 comes right from the stomach of the bug! Since the bug has -4 in its stomach for this problem, the factored form should look like
- (x - 4)2 = 11
Step 5: Eliminate the exponent. To counteract the square, take the square root of both sides; don't forget to stick a "±" sign on the right side and simplify that radical (if possible) when you do.
- x - 4 = ±11
You've Got Problems
Problem 2: Solve the equation by completing the square.
2 + 6x - 3 = 0
Step 6: Solve for x. In this problem, add 4 to both sides.
- x = 4 ± 11
So, the quadratic equation 2x2 - 16x + 10 = 0 has two solutions: x = 4 + 11 and x = 4 - 11; the "±" sign means that either sign will work for the expression.

Excerpted from The Complete Idiot's Guide to Algebra © 2004 by W. Michael Kelley. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
You can purchase this book at Amazon.com and Barnes & Noble.







