Geometry: Proving Lines Are Parallel
Proving Lines Are Parallel
CPOCTAC can be used to prove that line segments are congruent. It can also be used to prove that line segments are parallel. Recall that you have a couple of theorems to help you conclude that two lines are parallel. In Theorem 10.8 you learned that if two lines are cut by a transversal so that alternate interior angles are congruent, then those two lines are parallel. You will use this theorem in conjunction with CPOCTAC to show that line segments are parallel.
- Example 6: Suppose that ¯AC ~= ¯BD and ¯AB ~= ¯CD, as shown in Figure 12.13. Write a two-column proof to show that ¯AB ¯CD.
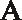
Figure 12.13¯AC ~= ¯BD and ¯AB ~= ¯CD
- Solution: Your game plan is to involve showing that ΔABC ~= ΔDCB. You have to be careful about how you write these triangles. It's easy to see that you will want ∠A and ∠D to correspond. It's a bit more difficult to see which other vertices need to be paired up. At this point, it would be wise to break the two triangles apart so that the relationships will be clearer. Check out Figure 12.14 to get a better idea of what is going on.

Figure 12.14The two triangles in Figure 12.13 broken apart.
Because ¯BC is congruent to itself, you can use the SSS Postulate to show that ΔABC ~= ΔDCB. You can then visualize Figure 12.18 as two lines, ↔AB and ↔CD, cut by a transversal ↔BC. Then not only are ∠ACB and ∠DBC corresponding angles (and therefore congruent) but they are also alternate interior angles. Because the alternate interior angles are congruent, you know that ¯AB ¯CD. You might want to read this paragraph again just to get a good feel for what you are about to do.
| Statements | Reasons | |
|---|---|---|
| 1. | ¯AC ~= ¯BD and ¯AB ~= ¯CD | Given |
| 2. | ¯BC ~= ¯BC | Reflexive property of ~= |
| 3. | ΔABC ~= ΔDCB | SSS Postulate |
| 4. | ∠ACB ~= ∠DBC | CPOCTAC |
| 5. | ↔AB and ↔CD are cut by a transversal ↔BC | Definition of transversal |
| 6. | ∠ACB and ∠DBC are alternate interior angles | Definition of alternate interior angles |
| 7. | ¯AB ¯CD | Theorem 10.8 |
Put Me in, Coach!
Here's your chance to shine. Remember that I am with you in spirit and have provided the answers to these questions in Answer Key.
- 1. Verify that ~= when applied to triangles is an equivalence relation.
- 2. If ¯AC ~= ¯CD and ∠ACB ~= ∠DCB as shown in Figure 12.15, prove that ΔACB ~= ΔDCB.

Figure 12.15¯AC ~= ¯CD and ∠ACB ~= ∠DCB.
- 3. If ¯CB ⊥ ¯AD and ∠ACB ~= ∠DCB , as shown in Figure 12.16, prove that ΔACB ~= ΔDCB.

Figure 12.16¯CB ⊥ ¯AD and ∠ACB ~= ∠DCB.
- 4. If ¯CB ⊥ ¯AD and ∠CAB ~= ∠CDB , as shown in Figure 12.17, prove that ΔACB ~= ΔDCB.

Figure 12.17¯CB ⊥ ¯AD and ∠CAB ~= ∠CDB.
- 5. If ¯CB ⊥ ¯AD and ¯AC ~= ¯CD, as shown in Figure 12.18, prove that ΔACB ~= ΔDCB.

Figure 12.18¯CB ⊥ ¯AD and ¯AC ~= ¯CD.
- 6. If ∠P ~= ∠R and M is the midpoint of ¯PR, as shown in Figure 12.19, prove that ∠N ~= ∠Q.

Figure 12.19∠P ~= ∠R and M is the midpoint of ¯PR.
Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







