Geometry: Prisms
Prisms
Suppose you have a polygon, like maybe a triangle or a rectangle, and you clone it. Now you have two congruent polygons lying side by side. If your polygons don't get along, and the plane isn't big enough for the both of them, one of them will have to move. Go ahead and move one of your polygons into a new plane. Don't twist it, or rotate it, or turn it in any way. Just lift it (or lower it, if you'd prefer) to a new plane that is parallel to the old plane. It doesn't have to be directly over (or under, if you chose to lower it) the other polygon; you can move it sideways if the spirit moves you. The goal is to have the two polygons in parallel planes, with the same orientation.
It's a well-known fact that absence makes the heart grow fonder. Now that your polygons have been separated, they might miss each other. That's not to say that they want to live in the same plane again. They might just want to establish some sort of connection. After all, these are congruent polygons, and the corresponding vertices might want to maintain their connection. Let's draw line segments connecting each pair of corresponding vertices. The result is a “solid” figure known as a prism. Two prisms (one based on a triangle, the other based on a rectangle) are shown in Figure 21.1. Notice that the two polygons lie in parallel planes.

Figure 21.1Two examples of prisms.
In order to talk about this new shape, I need to introduce you to some terms for the parts of a prism. The congruent polygons that lie in the parallel planes are the bases of the prism, and sides of these polygons are called the base edges. The line segments that connect the corresponding vertices of the congruent polygons are called the lateral edges of the prism. The polygons that are formed by the lateral edges are called the lateral faces of the prism. The vertices of the congruent polygons are the vertices of the prism. A prism will always have twice as many vertices as the base polygon.
Eureka!
A prism is the region formed by two parallel congruent polygons having corresponding vertices joined by line segments.
The bases of a prism are the congruent polygons that lie in the parallel planes.
The base edges of a prism are the edges of the base of the prism.
A vertex of a prism is a point of intersection of two base edges.
The lateral edges of a prism are the line segments connecting corresponding vertices of the bases of the prism.
A lateral face of a prism is the quadrilateral formed by a pair of corresponding base edges and the lateral edges that connect the corresponding vertices.
In the triangular prism, one of the two congruent triangles is directly over the other one. In this case the lateral edges are perpendicular to the base edges, and the prism is called a right prism. If the bases of a right prism are regular polygons (recall that a regular polygon is an equilateral and equiangular polygon), then the prism is called a regular prism.
In the rectangular prism (the prism created from congruent rectangles) shown in Figure 21.1, the lateral edges are not perpendicular to the base edges. This is an example of an oblique prism.
By now you might have noticed that a prism's name is related to the shape of its base. A triangular prism has a triangular base; a rectangular prism has a rectangular base, and so on. This pattern will be followed to the end of time (or at least until your ability to name polygons expires).
Solid Facts
A right prism is a prism in which the lateral edges are perpendicular to the base edges at the vertices.
An oblique prism is a prism in which the angle formed between a lateral edge and a base edge is not a right angle.
A regular prism is a right prism whose base is a regular polygon.
The most familiar prism is a cube. A cube is a prism with a square base. But that's just the beginning! The lateral edges of a cube are perpendicular to the base edges, so a cube is a right prism. But wait! There's more! The bases of a cube are squares, which are regular polygons. So a cube is a right prism whose base is a regular polygon. In other words, a cube is a regular prism. But there's more to a cube than that. A cube has lateral edges that are the same length as the base edges. That's enough to put a cube into a very elite category. It's in such an elite class that there are only five shapes worthy of admission. You'll learn more about that class at the end of this section.
Eureka!
To name a prism, start with the name of the polygon that forms its base. Next, determine if the base of the prism is a regular polygon. If it is, you have a regular prism. If not, you just have a run-of-the-mill, generic prism. Finally, determine if the lateral edges are perpendicular to the base edges. If they are, you have a right prism; otherwise you have an oblique prism. Put all of the pieces together and you have named that prism.
Prisms are named and classified by their bases and the relationship between their lateral edges and their base edges. Let's practice.
- Example 1: Name and classify each type of prism shown in Figure 21.2.
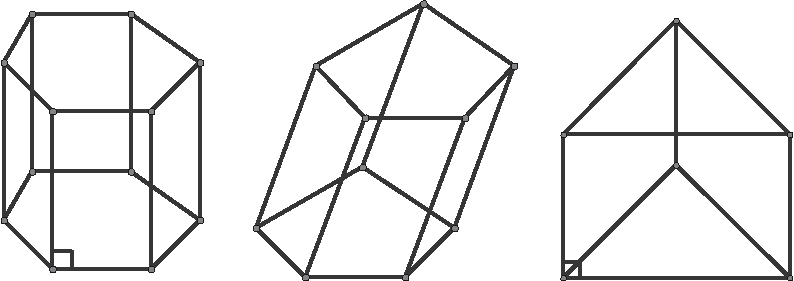
Figure 21.2Three prisms to name and classify.
- Solution: The first prism has a hexagonal base (not equilateral) and lateral edges perpendicular to the base edges. That makes it a right hexagonal prism. The second prism has a pentagonal base (not equilateral) and the lateral edges are not perpendicular to the base, so it's an oblique pentagonal prism. The third prism has a triangular base, and it is equilateral. By Theorem 14.3 it is also equiangular, which makes it regular. Because the lateral edges are perpendicular to the base edges, it is a right prism. Thus it is a right, regular, triangular prism.
Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







