Geometry: Calculating Areas
Calculating Areas
Recall that in order to calculate the area of a triangle, we needed to know its height, or the length of its altitude (a line segment drawn perpendicularly from a vertex to the opposite side), and the length of its base (the side perpendicular to the altitude). The areas of trapezoids and parallelograms will also be calculated using the lengths of their altitudes and bases.
Area of Trapezoids
Recall that the two parallel sides of a trapezoid are its bases. The area A of a trapezoid whose bases have lengths b1 and b2 and whose altitude has length h is given by
- A = 1/2h(b1 + b2).
Figure 15.11 shows trapezoid ABCD with bases ¯BC and ¯AD and altitude ¯BE.

Figure 15.11Trapezoid ABCD whose bases have lengths b1 and b2 and whose altitude has length h.
- Example 5: Find the area of the trapezoid in Figure 15.11 if BC = 8, AD = 14, and BE = 5.
- Solution: Because the area of a trapezoid is A = 1/2h(b1 + b2), you can substitute our values for the height and the two bases. A = 1/2(5)(8 + 14), or A = 55 units2.
Area of Parallelograms
There are a couple of methods for finding the area of a parallelogram, depending on the kind of parallelogram you are working with. The parallelogram shown in Figure 15.13 has an altitude of length h and a base of length b. Its area A can be calculated using the formula A = bh.

Figure 15.12Parallelogram ABCD has an altitude of length h and a base of length b.
- Example 6: Find the area of the parallelogram in Figure 15.12 if AD = 14 and BE = 5.
- Solution: Using the equation for area, A = bh, A = 14 × 5 = 70 units2.
This formula works with any parallelogram. If you are dealing with a rectangle, then the altitude corresponds to one of the sides of the rectangle and the base corresponds to one of its adjacent sides. So the area of a rectangle is the product of the lengths of two adjacent sides. If you are working with a square, then adjacent sides are congruent, so the area is the square of the length of one of its sides.
Whenever you are working with a quadrilateral whose diagonals are perpendicular, you can relate the area of the quadrilateral to the lengths of its diagonals. The quadrilateral ABCD in Figure 15.13 has diagonals of length dand d. Its area can be calculated using the formula
- A = 1/2d1d2.
Eureka!
The area of a rectangle can be found by taking the product of the lengths of two consecutive sides. The area of a square is found by squaring the length of one of its sides.
This equation can be used for rhombuses and squares, and any other quadrilateral that has perpendicular diagonals, like kites.
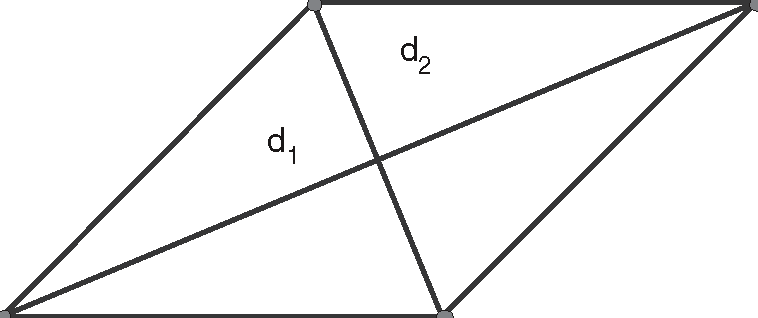
Figure 15.13Quadrilateral ABCD with diagonals of length d1 and d2.
- Example 7: Find the area of a rhombus ABCD with diagonals of length 8 and 12.
- Solution: Substituting into the equation for area, A = 1/2d1d2, you have A = 1/2(8)(12), or A = 48 units2.
The Pythagorean Theorem (again)
Now that you can compute the area of a square (it's just the square of the length of one of its sides), you can prove the Pythagorean Theorem again. Suppose we have a right triangle with legs of length a and b and the hypotenuse with length c as shown in Figure 15.14. Then by the Pythagorean Theorem, a2 + b2 = c2.
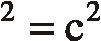
Figure 15.14A right triangle with legs of length a and b and the hypotenuse with length c.
Arrange four copies of these triangles as shown in Figure 15.15. Then form two squares: a big square with side length a + b and a small square of side length c. The area of the big square can be calculated in two ways. The first way is to compute the square of the length of the side: (a + b)2.

Figure 15.15Four copies of ΔABC arranged to help prove the Pythagorean Theorem.
The second way is to add up the areas of the four triangles and the small square. The area of a right triangle is just one-half the product of the lengths of the legs:
- 1/2ab,
and the area of the small square is c2. Because both of these methods for finding the area of the big square should give the same result, you have the following equation:
- (a + b)2 = 4(1/2ab) + c2
Expanding your terms and rearranging yields the Pythagorean Theorem:
- a2 + 2ab + b2 = 2ab + c2
- a2 + b2 = c2
That's quite a slick proof of the Pythagorean Theorem, in my humble opinion. All you needed was a clever arrangement of four copies of the triangle and the ability to compute the areas of a triangle and a square.
Here's your chance to shine. Remember that I am with you in spirit and have provided the answers to these questions in Answer Key.
- 1. In trapezoid ABCD, ¯BC ¯AD , R is the midpoint of ¯AB , and S is the midpoint of ¯CD , as shown in Figure 15.16. Find AD, BC, and RS if BC = 3x, RS = 4x + 9, and AD = 10x − 27.

Figure 15.16Trapezoid ABCD. ¯BC ¯AD, ¯AB has midpoint R, and ¯CD has midpoint S.
- 2. There are three other altitudes of trapezoid ABCD shown in Figure 15.4. Can you find them?
- 3. Write a proof of Theorem 15.3.
- 4. Write a proof of Theorem 15.4.
- 5. Write a two-column proof of Theorem 15.7.
- 6. Find the area of the trapezoid in Figure 15.11 if BC = 12, AD = 20 and BE = 9.
- 7. Find the area of the parallelogram in Figure 15.12 if AD = 20 and BE = 9.
- 8. Find the area of the parallelograms in Figure 15.17.

Figure 15.17Compute the areas of the following parallelograms.
Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.







